| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
The scalar product of two vectors
![]() and
and ![]() is a scalar.
is a scalar.
Its value is:
![]()
![]()
![]()
![]()
![]()
![]() .
.
The scalar product is commutative:
![]()
![]()
![]()
![]() (1.3)
(1.3)![]()
The vectorial
product of two vectors ![]() and
and ![]() is a
vector perpendicular on the plane determined by those vectors, directed in such
a manner that the trihedral
is a
vector perpendicular on the plane determined by those vectors, directed in such
a manner that the trihedral ![]()
![]() and
and ![]() should be
rectangular.
should be
rectangular.
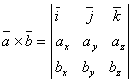
The modulus of the vectorial product is given by the relation:
![]()
The vectorial product is non-commutative:
![]()
The mixed product of
three vectors ![]() ,
,![]() and
and ![]() is a scalar.
is a scalar.
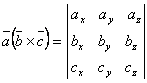
The double vectorial product of three vectors ![]() ,
,![]() and
and ![]() is a vector situated in the plane
is a vector situated in the plane ![]() .
.
The formula of the double vectorial product:
![]()
The operator
![]() is defined
by:
is defined
by:
![]()
![]() applied to a scalar is called gradient.
applied to a scalar is called gradient. ![]()
![]() (1.10)
(1.10)
![]() scalary applied to a vector is called
divarication.
scalary applied to a vector is called
divarication. ![]()
![]() (1.11)
(1.11)
![]() vectorially applied to a vector is called
rotor.
vectorially applied to a vector is called
rotor. ![]()
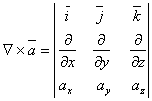
Operations
with ![]() :
:
![]() (1.13)
(1.13)
![]() (1.14)
(1.14)
![]() (1.15)
(1.15)
When ![]() acts upon a
product:
acts upon a
product:
in the first place has differential and only then vectorial proprieties;
all the vectors or the scalars upon which it doesnt act must, in the end, be placed in front of the operator;
it mustnt be placed alone at the end.
![]() (1.16)
(1.16)
![]() (1.17)
(1.17)
![]() (1.18)
(1.18)
![]() (1.19)
(1.19)
![]() (1.20)
(1.20)
![]() (1.21)
(1.21)
![]() (1.22)
(1.22)
![]() (1.23)
(1.23)
![]() the scalar
the scalar ![]() considered constant,
considered constant,
![]() -
the scalar
-
the scalar ![]() considered constant,
considered constant,
![]() -
the vector
-
the vector ![]() considered
constant,
considered
constant,
![]() -
the vector
-
the vector ![]() considered
constant.
considered
constant.
If:
![]() (1.24)
(1.24)
then:
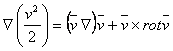 (1.25)
(1.25)
The
streamline is a curve tangent in each of its points to the velocity vector of
the corresponding point ![]() .
.
The equation of the streamline is obtained by writing that the tangent to streamline is parallel to the vector velocity in its corresponding point:
![]() (1.26)
(1.26)
The
whirl line is a curve tangent in each of its points to the whirl vector of the
corresponding point ![]() .
.
![]() (1.27)
(1.27)
The equation of the whirl line is obtained by writing that the tangent to whirl line is parallel with the vector whirl in its corresponding point:
![]() (1.28)
(1.28)
Gauss-Ostrogradskis relation:
![]() (1.29)
(1.29)
where
![]() -
volume delimited by surface
-
volume delimited by surface ![]() .
.
The circulation of velocity on a curve (C) is defined by:
![]()
![]() (1.30)
(1.30)
in which
![]() (1.31)
(1.31)
represents
the orientated element of the curve (![]() - the versor
of the tangent to the curve (C )).
- the versor
of the tangent to the curve (C )).
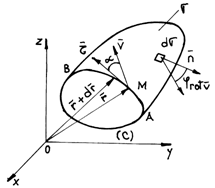
Fig.1.1
![]() (1.32)
(1.32)
The sense of circulation depends on the admitted sense in covering the curve.
![]() (1.33)
(1.33)
Also:
![]() (1.34)
(1.34)
Stokes relation:
![]() (1.35)
(1.35)
in
which ![]() represents the versor of the normal to the
arbitrary surface
represents the versor of the normal to the
arbitrary surface ![]() bordered by the curve (C).
bordered by the curve (C).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1267
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved