| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
In this chapter we shall present the hydraulic calculus of conduits under pressure in a permanent regime.
Conduits under pressure are in fact a hydraulic system designed to transport fluids between two points with different energetic loads.
Conduits can be simple (made up of one or several sections of the same diameter or different diameters), or with branches, in this case, setting up networks of distribution.
By the manner in which the outcoming of the fluid from the conduit is made, we distinguish between conduits with a free outcome, which discharge the fluid in the atmosphere (fig.8.1 a) and conduits with chocked outcoming (fig. 8.1 b).
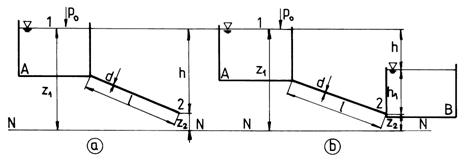
Fig.8.1a, b
If we write Bernoullis equation for a stream of real liquid, between the free side of the liquid from the tank A and the end of the conduit, taking as a reference plane the horizontal plane N N, we get:
![]() (8.1)
(8.1)
which, for the case presented
in fig.8.1 a, when ![]() ,
, ![]() ,
, ![]() ,
, ![]() , becomes:
, becomes:
![]() (8.2)
(8.2)
where ![]() is the mean velocity in the section of the
conduit , and h is the load of the conduit.
is the mean velocity in the section of the
conduit , and h is the load of the conduit.
In the analysed case shown in fig. 8.1 b, by introducing in
equation (8.1) the relations ![]() and
and ![]() , we shall
get the expression (8.2).
, we shall
get the expression (8.2).
From
an energetic point of view, this relation shows that from the available specific
potential energy (h), a part is transformed into specific kinetic energy (![]() ) of the
stream of fluid, which for the given conduit is lost at the outcoming in the
atmosphere or in another volume. The other part
) of the
stream of fluid, which for the given conduit is lost at the outcoming in the
atmosphere or in another volume. The other part ![]() is used to overcome the hydraulic resistances
(that arise due to the tangent efforts developed by the fluid in motion) and is
lost because it is irreversibly transformed into heat.
is used to overcome the hydraulic resistances
(that arise due to the tangent efforts developed by the fluid in motion) and is
lost because it is irreversibly transformed into heat.
Analysing the losses of load from the conduit we shall divide them into two categories, writing the relation:
![]() (8.3)
(8.3)
The losses of load, denoted by ![]() are brought about by the tangent efforts that
are developed during the motion of the fluid along the length of the conduit (
l) and, for this reason, they are called losses of load distributed. These
losses of load have been determined in paragraph 7.4.2, getting the relation
(7.54) which we may write in the form:
are brought about by the tangent efforts that
are developed during the motion of the fluid along the length of the conduit (
l) and, for this reason, they are called losses of load distributed. These
losses of load have been determined in paragraph 7.4.2, getting the relation
(7.54) which we may write in the form:
![]() (8.4)
(8.4)
where
the coefficient of losses of load, ![]() , called Darcy coefficient is determined by
the relations shown in table 7.1 ; the manner of calculus being also shown in
that paragraph. Generally, in practical cases, the values of coefficient
, called Darcy coefficient is determined by
the relations shown in table 7.1 ; the manner of calculus being also shown in
that paragraph. Generally, in practical cases, the values of coefficient ![]() vary in a domain that ranges between
vary in a domain that ranges between ![]() .
.
Being proportional to the length of the conduit, the distributed losses of load are also called linear losses.
The second category of losses of load is represented by the local losses of load that are brought about by: local perturbation of the normal flow, the detachment of the stream from the wall, whirl setting up, intensifying of the turbulent mixture, etc; and arise in the area where the conduit configuration is modified or at the meeting an obstacle detouring (inlet of the fluid in the conduit, flaring, contraction, bending and derivation of the stream, etc.).
The local losses of load are calculated with the help of a general formula, given by Weissbach:
![]() (8.5)
(8.5)
where
![]() is the local loss of load coefficient that is
determined for each local resistance (bends, valves, narrowing or enlargements
of the flow section etc.).
is the local loss of load coefficient that is
determined for each local resistance (bends, valves, narrowing or enlargements
of the flow section etc.).
Generally, coefficient ![]() depends mainly on the geometric parameters of
the considered element, as well as on some factors that characterise the
motion, such as: the velocities distribution at the inlet of the fluid in the
examined element, the flow regime, Reynolds number etc.
depends mainly on the geometric parameters of
the considered element, as well as on some factors that characterise the
motion, such as: the velocities distribution at the inlet of the fluid in the
examined element, the flow regime, Reynolds number etc.
In practice, coefficient ![]() is determined with respect to the type of the
respective local resistance, using tables, monograms or empirical relations
that are found in hydraulic books. Therefore, for curved bends of angle
is determined with respect to the type of the
respective local resistance, using tables, monograms or empirical relations
that are found in hydraulic books. Therefore, for curved bends of angle ![]() ,
coefficient
,
coefficient ![]() can be determined by using the relation:
can be determined by using the relation:
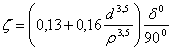 (8.6)
(8.6)
where
![]() are the diameter and curvature radius of the
bend, respectively.
are the diameter and curvature radius of the
bend, respectively.
Coefficient ![]() ,
corresponding to the loss of load at the inlet in their conduit, depends mainly
on the wall thickness of the conduit with respect to its diameter and on the
way the conduit is attached to the tank. If the conduit is embedded at the
level of the inferior wall of the tank, the losses of load that arise at the
inlet in the conduit are equivalent with the losses of load in an exterior
cylindrical nipple. For this case,
,
corresponding to the loss of load at the inlet in their conduit, depends mainly
on the wall thickness of the conduit with respect to its diameter and on the
way the conduit is attached to the tank. If the conduit is embedded at the
level of the inferior wall of the tank, the losses of load that arise at the
inlet in the conduit are equivalent with the losses of load in an exterior
cylindrical nipple. For this case, ![]() .
.
If on the route of the conduit there are several local resistances, the total loss of fluid will be given by the arithmetic sum of the losses of load corresponding to each local resistance in turn, namely:
![]() (8.7)
(8.7)
Using relations (8.4) and (8.7), we get the total loss of load of the conduit:
![]() (8.8)
(8.8)
that allows us to write relation (8.2) in the form:
![]() (8.9)
(8.9)
where from the mean velocity in the flow section will result:
 (8.10)
(8.10)
The flow of the conduit is determined by:
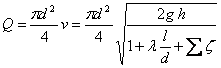 (8.11)
(8.11)
which allows us to express the load of the conduit, h, and diameter, d, with respect to flow Q; we get:
![]() (8.12)
(8.12)
and respectively:
![]() (8.13)
(8.13)
Sometimes in the calculus of enough long conduits, the kinetic term ![]() and the local losses of load are negligible
with respect to the linear losses of load.
and the local losses of load are negligible
with respect to the linear losses of load.
In the case of such conduits, called long conduits, relation (8.2) takes the form:
![]() (8.14)
(8.14)
and relations (8.10), (8.11), (8.12) and (8.13) become:
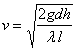 (8.15)
(8.15)
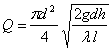 (8.16)
(8.16)
![]() (8.17)
(8.17)
and, respectively:
![]() (8.18)
(8.18)
With the help of the above written relations all problems concerning the computation of conduits under pressure can be solved. Generally, these problems are divided into three categories:
a) to determine the load of the conduit, when length, rugosity, flow and rugosity of interior walls of the conduit are known;
b) to determine the optimal diameters when flow, length, rugosity of the walls of conduit as well as the admitted load are known;
c) to determine the flow of liquid conveyed through the conduit when diameter, length, nature of the wall of conduit and its load are known.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1460
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved