| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
We
take into consideration a volume ![]() of fluid.
This fluid is homogeneous, incompressible, of density
of fluid.
This fluid is homogeneous, incompressible, of density ![]() , bordered
by surface
, bordered
by surface ![]() . The
elementary volume
. The
elementary volume ![]() has the speed
has the speed ![]() .
.
The elementary impulse will be:
![]() (6.1)
(6.1)
![]() (6.2)
(6.2)
![]() (6.3)
(6.3)
At the same time
![]() (6.4)
(6.4)
But:
![]() (dAlembert
principle). (6.5)
(dAlembert
principle). (6.5)
Therefore:
![]() (6.6)
(6.6)
The total derivative, of the impulse with respect to time, is equal to
the resultant ![]() of the exterior forces, or
of the exterior forces, or
![]() , (6.7)
, (6.7)
where
![]() are the mass flows through entrance/ exit
surfaces.
are the mass flows through entrance/ exit
surfaces.
Under permanent flow conditions of ideal fluid, the vectorial sum of the
external forces which act upon the fluid in the volume ![]() , is equal
with the impulse flow through the exit surfaces (from the volume
, is equal
with the impulse flow through the exit surfaces (from the volume ![]() ), less the
impulse flow through the entrance surfaces (to the volume
), less the
impulse flow through the entrance surfaces (to the volume ![]() ) .
) .
![]() -
the position vector of the centre of volume with respect to origin of the
reference system.
-
the position vector of the centre of volume with respect to origin of the
reference system.
The elementary inertia moment with respect to point O (the origin) is:
![]() (6.8)
(6.8)
since
![]() (6.9)
(6.9)
then
![]() (6.10)
(6.10)
If:
![]() the elementary impulse, (6.11)
the elementary impulse, (6.11)
![]() the moment of elementary impulse, (6.12)
the moment of elementary impulse, (6.12)
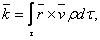 (6.13)
(6.13)
![]() (6.14)
(6.14)
The derivative of the resultant moment of impulse with respect to time is equal with the resultant moment of inertia forces with reversible sign.
![]() (6.15)
(6.15)
where
![]() -
the moment of mass forces,
-
the moment of mass forces,
![]() -
the moment pressure forces,
-
the moment pressure forces,
![]() -
the moment of external forces.
-
the moment of external forces.
![]() -
the position vector of the centre of gravity for the exit /entrance surfaces.
-
the position vector of the centre of gravity for the exit /entrance surfaces.
![]() (6.16)
(6.16)
Under permanent flow conditions of ideal
fluids, the vectorial addition of the moments of external forces which act upon
the fluid in the volume ![]() , is equal
to the moment of the impulse flow through the exit surfaces less the moment of
the impulse flow through the entrance surfaces.
, is equal
to the moment of the impulse flow through the exit surfaces less the moment of
the impulse flow through the entrance surfaces.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1572
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved