Scrigroup - Documente si articole

     

 
HomeDocumenteUploadResurseAlte limbi doc
 
BulgaraCeha slovacaCroataEnglezaEstonaFinlandezaFranceza
GermanaItalianaLetonaLituanianaMaghiaraOlandezaPoloneza
SarbaSlovenaSpaniolaSuedezaTurcaUcraineana

ēkaģeogrāfijaķīmijaBioloģijaBiznessDažādiEkoloģijaEkonomiku
FiziskāsGrāmatvedībaInformācijaIzklaideLiteratūraMākslaMārketingsMatemātika
MedicīnaPolitikaPsiholoģijaReceptesSocioloģijaSportaTūrismsTehnika
TiesībasTirdzniecībaVēstureVadība

Stereometrijas pamatjēdzieni, paralelitate un perpendikularitate telpa

matemātika



+ Font mai mare | - Font mai mic



DOCUMENTE SIMILARE

Stereometrijas pamatjēdzieni, paralelitate un perpendikularitate telpa



Risinam kopa

1.uzdevums

Attalums no punkta A līdz plaknei a ir 8 cm. No punkta A pret plakni a novilktas divas vienada garuma slīpnes AK un AL, kuras sava starpa veido 600 lielu leņķi. Leņķis starp slīpni AK un perpendikulu ir 450. Apēķini attalumu starp slīpņu pamatiem!

Atrisinajums

DKAO – vienadsanu taisnleņķa trijstūris, KO = AO = 8cm

Þ Pēc Pitagora teorēmas

Vai

Þ DAKL – vienadmalu, jo AK = AL pēc dota, leņķis KAL ir 600 pēc dota, tatad .

Atbilde

2.uzdevums

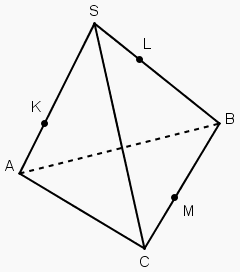
Uzzīmē dota tetraedra SABC šķēlumu ar plakni, kas iet caur punktiem K, L un M, kuri atrodas uz tetraedra šķautnēm!

IT_11_05_04

Atrisinajums

Animacija

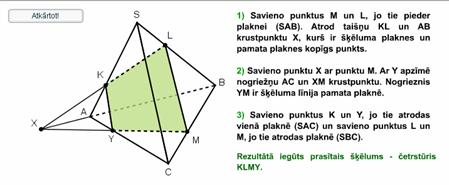
IT_11_05_05

Atbilde

šķēlums – četrstūris KYML

3.uzdevums

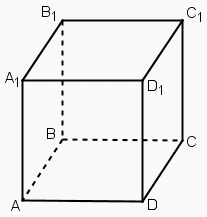
Dots kubs ABCDA1B1C1D1. Nosaki leņķi starp skaldni BB1C1C un šķēlumu AA1C1C!

IT_11_05_06

Atrisinajums

Animacija

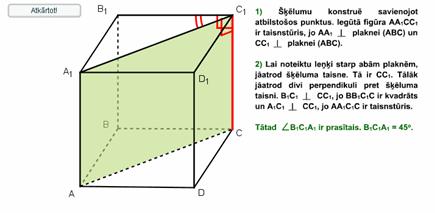
IT_11_05_07

Atbilde

ÐB1C1A1 = 450.

Risini pats

1.uzdevums

Aizpildi shēmu!

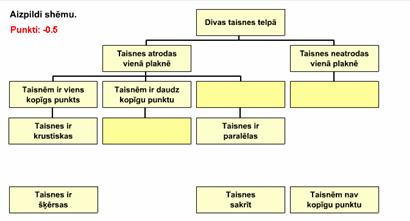
IT_11_05_08

2.uzdevums

Aizpildi shēmu!

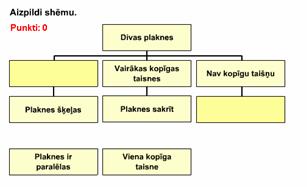
IT_11_05_09

3.uzdevums

Dots kubs ABCDA1B1C1D1. Nosaki leņķi:

a)      starp skaldni ABCD un šķēlumu A1B1CD;

b)      starp šķēlumiem AA1C1C un BB1D1D.

Atbilde

a) ÐA1DA = 450.

b) ÐAOD = 900.

4.uzdevums

No punkta pret plakni ir novilkta gara slīpne. Aprēķinat leņķi starp slīpni un plakni, ja slīpnes projekcija ir 1,5 cm gara.

Atbilde

5.uzdevums

No kvadrata ABCD virsotnes A pret ta plakni novilkts perpendikuls AK. Attalumi no K līdz kvadrata malam BC un CD ir 10 cm, bet līdz virsotnei C – 14 cm. Aprēķinat attalumu no K līdz kvadrata plaknei.

Atbilde

KA = 2cm

6.uzdevums

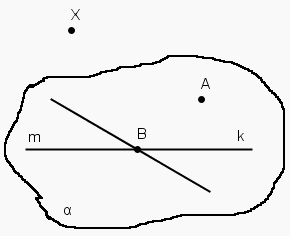
Pieraksti zīmējuma doto informaciju, izmantojot simbolisko pierakstu!

IT_11_05_11

Atbilde

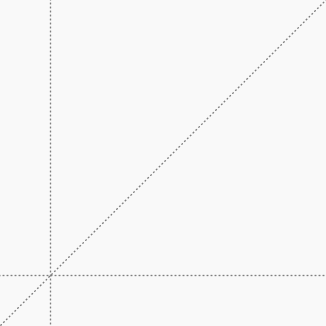7.uzdevums

Izmantojot paralēlo projekciju īpašības, paskaidro, ka var uzkonstruēt jebkuru paralēlskaldni! Pabeidz zīmējumu, konstruējot paralēlskaldni, ja dotas trīs šķautnes, kas neatrodas viena plaknē un krustojas viena punkta.

IT_11_05_12

Atbilde

Animacija

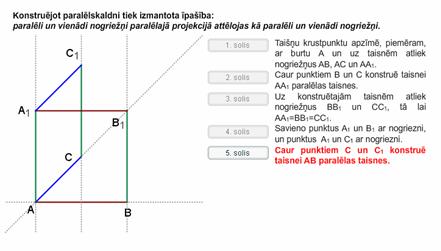
IT_11_05_13

8.uzdevums

Dots kubs ABCDA1B1C1D1. Kads ir noradīto taišņu novietojums?

Animacija

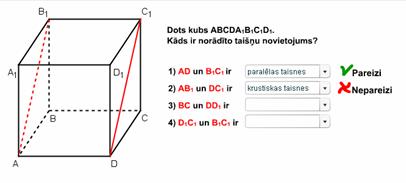
IT_11_05_10

Parbaudi sevi

1. Punkts M nepieder taisnei a. Cik taišņu var novilkt caur punktu M ta, lai tas nekrusto taisni a?

A tikai vienu

B nevienu

C tikai divas

D bezgalīgi daudz

2. Punkts M nepieder plaknei a. Cik plakņu var novilkt caur punktu M, kas paralēlas plaknei a

A vienu

B nevienu

C divas

D bezgalīgi daudz

3. Ja divam taisnēm telpa nav kopīgu punktu, tad tas ir:

A tikai paralēlas

B tikai šķērsas

C krustiskas

D paralēlas vai šķērsas

4. Cik divplakņu kaktu ir tetraedram?

A 3 B 4 C 7 D 6

5. Taisne a krusto plakni a punkta M, bet taisne b ir paralēla plaknei a. Kads var būt taišņu a un b savstarpējais novietojums?

A tikai šķērsas

B tikai krustiskas

C šķērsas vai krustiskas

D paralēlas vai krustiskas

6. ABCD – taisnstūris, CK ABCD. Kada nogriežņa garums nosaka punkta K attalumu līdz taisnstūra malai AB?

A KA

B CB

C CA

D KB

7. No punkta K, kas neatrodas plaknē a, novilkta slīpne KA un perpendikuls KO. Kads ir slīpnes KA projekcijas garums, ja KA 10 cm, KO 8 cm:

A 2 cm

B cm

C 18 cm

D 6 cm 

8. Kuri apgalvojumi ir aplami?

I jebkuri trīs punkti atrodas viena plaknē;

II caur jebkuriem četriem punktiem var novilkt plakni;

III caur jebkuriem trim punktiem var novilkt tikai vienu plakni;

IV taisne, kas neatrodas plaknē, krusto šo plakni;

V caur jebkuriem trim punktiem, kas neatrodas uz vienas taisnes, var novilkt plakni.

A II, III

B IV, V

C II, III, IV

D I, V

9. Kuri no dotajiem apgalvojumiem ir patiesi?

Var novilkt plakni, pie tam tikai vienu:

I caur trim punktiem, kas neatrodas uz vienas taisnes;

II caur taisni un punktu, kas neatrodas uz taisnes;

III caur divam krustiskam taisnēm;

IV caur divam šķērsam taisnēm;

V caur divam paralēlam taisnēm.

A I, II, III

B I, III, V

C I, II, III, V

D II, III, V

10. ABCDA1B1C1D1 – kubs. Punkti E un F ir attiecīgi šķautņu AA1 un CC1 viduspunkti. Nosaki kuba un plaknes, kuru nosaka punkti B, E un F šķēluma malu skaitu!

A 3 B 4 C 5 D 6

11. Ja ABCDA1B1C1D1 – kubs un K– AB viduspunkts, M – AD viduspunkts, tad no apgalvojumiem:

I ÐAB1C

II KM B1C patiesi ir

A I, II

B I

C II

D neviens

12. Taisne, kas novilkta plaknē caur slīpnes pamatu perpendikulari slīpnes projekcijai šaja plaknē, ir perpendikulara arī pašai slīpnei. Dotais apgalvojums ir:

A taisnes un plaknes perpendikularitates nosacījums;

B taisnes un plaknes paralelitates nosacījums;

C triju perpendikulu teorēma;

D plakņu paralelitates nosacījums.

13. Leņķis starp vienadmalu trijstūra ABK un kvadrata ABCD plaknēm ir 90 . Noteikt attalumu KD, ja AB 6 m.

A m

B m

C m

D m

14. ABCDA1B1C1D1 ir kubs. Plakņu A1B1C un B1C1D šķēlums ir:

A taisne A1C

B plakne A1B1C

C taisne B1D

D plakne ADB1

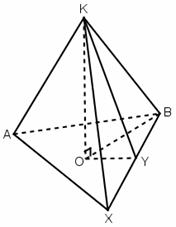15. Zīmējuma redzams tetraedrs KABX. Leņkis, ko veido sanu šķautne ar pamata plakni ir :

A KBY

B KBO

C KYO

D BKO

IT_11_05_01

16. Paralēlaja projekcija taisnstūra attēls ir:

A taisnstūris

B kvadrats

C trapece

D paralelograms

D

A

D

D

C

D

D

C

C

B

D

C

C

C

B

D

Komentari

6. saskaņa ar triju perpendikulu teorēmu.

14. B1 ir abu plakņu kopīgais punkts pēc dota, bet D ir abu plakņu kopīgais punkts pēc konstrukcijas, tapēc B1D ir šo plakņu šķēluma taisne.


Politica de confidentialitate | Termeni si conditii de utilizare



DISTRIBUIE DOCUMENTUL

Comentarii


Vizualizari: 6628
Importanta: rank

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved