| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
The fluid statics hydrostatics is that part of the mechanics of fluid which studies the repose conditions of the fluid as well as their action, during the repose state, on solid bodies with whom they come into contact.
Hydrostatics is identical for real and ideal fluids, as viscosity becomes manifest only during motion. In hydrostatics the notion of time does no longer exist.
If in Eulers equation (3.9) we assume
that ![]() , we get:
, we get:
![]() (4.1)
(4.1)
We multiply everywhere by ![]() :
:
![]() (4.2)
(4.2)
or
![]() (4.3)
(4.3)
If the axis ![]() of the system
of the system ![]() is vertical, upwards directed, then:
is vertical, upwards directed, then:
![]()
![]()
and equation (4.3) becomes:
![]() (4.4)
(4.4)
In the case of liquids (![]() = cons.), by
integrating equation (4.4) we get:
= cons.), by
integrating equation (4.4) we get:
![]() (4.5)
(4.5)
or
![]() (4.6)
(4.6)
or
![]() (4.7)
(4.7)
Equation (4.7) is called the fundamental equation of hydrostatics.
If ![]() is the
pressure at the surface of water (in open tank the atmospheric pressure),
pressure p, situated at a distance h from the surface, will be (fig.4.1):
is the
pressure at the surface of water (in open tank the atmospheric pressure),
pressure p, situated at a distance h from the surface, will be (fig.4.1):
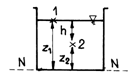
Fig.4.1
![]() (4.8)
(4.8)
![]() (4.9)
(4.9)
p is called the absolute pressure in
the point 2, and ![]() is the relative pressure.
is the relative pressure.
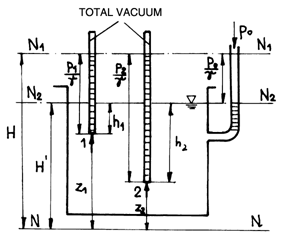
Fig.4.2
According to (4.6) we can write:
![]() (4.10)
(4.10)
In fig.4.2 we have:
![]() - piezometric height corresponding to the absolute hydrostatic pressure;
- piezometric height corresponding to the absolute hydrostatic pressure;
![]() - the quotes to an arbitrary plane
(position heights).
- the quotes to an arbitrary plane
(position heights).
We rewrite the fundamental equation of hydrostatics between two points 1 and 2.
![]() (4.11)
(4.11)
Supposing that in point 1, the
pressure registers a variation ![]() , it becomes
, it becomes
![]() . In order
that the equilibrium state shouldnt be altered, for point 2 the same variation of pressure has to be
registered.
. In order
that the equilibrium state shouldnt be altered, for point 2 the same variation of pressure has to be
registered.
![]() (4.12)
(4.12)
Hence:
![]() (4.13)
(4.13)
Pascals principle:
Any pressure variation created in a certain point in a non-compressible liquid in equilibrium, is transmitted with the same intensity to each point in the mass of this liquid.
Let us consider two communicating
vessels (fig.4.3) that contain two non-miscible liquids, which have specific
weights ![]() and
and ![]() ,
respectively. Writing the equality of pressure in the points 1 and 2, situated
in the same horizontal plane N N that also contains the separation surface
between the two liquids, we get:
,
respectively. Writing the equality of pressure in the points 1 and 2, situated
in the same horizontal plane N N that also contains the separation surface
between the two liquids, we get:
![]() (4.14)
(4.14)
or else
![]() (4.15)
(4.15)
where ![]() and
and ![]() are the heights of the two liquid columns
that, according to this relation, are in reverse proportion to the specific
weights of the two liquids.
are the heights of the two liquid columns
that, according to this relation, are in reverse proportion to the specific
weights of the two liquids.
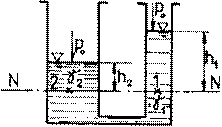
Fig.4.3
If ![]()
then ![]() .
.
In two or more communicating vessels, that contain the same liquid (homogenous and non-compressible), their free surfaces are on the same horizontal plane.
The pressure force that acts upon a solid wall is determined by means of the relation:
![]() (4.16)
(4.16)
where dA is
a surface element having the versor ![]() , and p is
the relative pressure of the fluid.
, and p is
the relative pressure of the fluid.
Let A be a
vertical plane surface that limits a non-compressible fluid, with specific
weight ![]() (fig.4.4).
(fig.4.4).
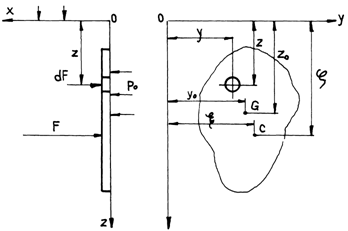
Fig.4.4
Then the hydrostatic pressure force will be:
![]() (4.17)
(4.17)
where:
![]() - the quote of the specific weight for surface
A;
- the quote of the specific weight for surface
A;
![]() - the static moment of the surface A
with respect to the axis Oy.
- the static moment of the surface A
with respect to the axis Oy.
The application point of the pressure force F is called pressure centre. It has the following co-ordinates:
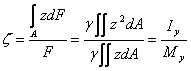 (4.18)
(4.18)
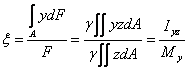
![]() - the inertia moment of surface A with respect
to the axis Oy;
- the inertia moment of surface A with respect
to the axis Oy;
![]() - the centrifugal moment of surface
A with respect to axes Oy and Oz.
- the centrifugal moment of surface
A with respect to axes Oy and Oz.
The hydrostatic pressure force that acts upon the bottom of a container does not depend on the quantity of liquid, but on the height of the liquid and on the section of the bottom of this container.
The above statement represents the hydrostatic paradox and is illustrated in fig.4.5. The force that presses on the bottom of the three different shaped containers, is the same because the level of the liquid in the container is the same, and the surface of the bottom is the same.
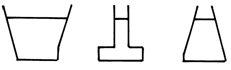
Fig. 4.5
Lets consider a solid body and further to simplify a cylinder, submerged in a liquid; we intend to compute the resultant of the pressure forces that act upon it (fig.4.6).
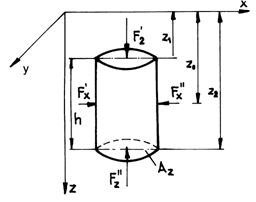
Fig.4.6
The resultant of the horizontal
forces ![]() and
and ![]() is obviously nil:
is obviously nil:
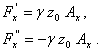 (4.19)
(4.19)
The vertical forces will have the value:
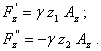 (4.20)
(4.20)
Thus their resultant will be:
![]() (4.21)
(4.21)
This demonstration may easily be extended for a body of any shape.
An object submerged in a liquid is up thrust with an equal force with the weight of the displaced liquid.
A free body, partially submerged in a liquid is called a floating body.
The submerged part is called immerse part or hull.
The weight centre of the hulls volume is called the hull centre.
The free surface of the liquid is called floating plane.
The crossing between the floating plane and the floating body is called the floating surface.
Its weight centre is called floating centre, and its outline is called floating line or water line.
In order that the floating body be in equilibrium, it is necessary that the sum of the forces that act upon it as well as the resultant moment should be nil.
Upon a floating body there can act two forces: the archimedean force and the weight force also called displacement (D = mg) (fig.4.7)
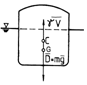
Fig.4.7
As a result, a first condition to achieve the equilibrium is:
![]() , (4.22)
, (4.22)
where m is the mass of the floating body, V is the
volume of the hull, and ![]() is the specific weight of the liquid.
is the specific weight of the liquid.
Furthermore, in order that the moment of the resultant should be nil these two forces must have the same straight line as support or, in other words, that the weight centre G should be found on the same vertical with the centre hull.
Equation (4.22) is called the equation of flotability.
Stability is the ability of the floating body to return on the initial floating of equilibrium after the action of perturbatory forces that drew it out of that position has ceased.
With respect to a Cartesian system of axes Oxyz, having the plane xOy in the floating plane and axis Oz upwards directed (fig.4.8), the floating body has six degrees of freedom: three translations and three rotations. The rotation around Ox and Oy is most important.
These slantings are due to the actions of waves or wind.
By definition, the rotation of the floating body thus produced as the volume of the hull to remain unchanged as a value but which can vary in shape is called isohull slanting.
Let ![]() be the plane of the initial floating. After
the slanting of the isohull around a certain axis, the floating body will be on
a floating
be the plane of the initial floating. After
the slanting of the isohull around a certain axis, the floating body will be on
a floating ![]() .
.
If
initially the centre of hull were situated in the point ![]() after the isohull slating with an angle
after the isohull slating with an angle ![]() , the centre
of hull would move
, the centre
of hull would move
further, in the sense of slanting, to a point ![]() .
.
This movement takes place due to the alteration of the shape of the hull volume.
The locus of the successive positions of the centre of the hull for different isohull slantings around the same axis is called the curve of the centre of hull (trajectory C).
The curvature centre of the curve of the hull centres is called metacentre and its curvature radius is called metacentric radius.
For transversal slantings around the longitudinal axis Ox we shall talk about a transversal metacentre M and about a transversal metacentric radius r (fig.4.8 a).
Fig.4.8 a, b
For
longitudinal slantings around the transversal axis Oy the longitudinal
metacentre will be denoted by ![]() , and the
corresponding metacentric radius will be R (fig. 4.8 b).
, and the
corresponding metacentric radius will be R (fig. 4.8 b).
Causing a transversal slanting to
the floating body, isohull, with a small angle, ![]() , the centre of hull will move to point
, the centre of hull will move to point ![]() (fig.4.8 a). In this case, the force of
flotability
(fig.4.8 a). In this case, the force of
flotability ![]() , normal on
the slanting flotability
, normal on
the slanting flotability ![]() , having as
application point the point
, having as
application point the point ![]() wont have
the same support as the weight (displacement) of the floating body.
wont have
the same support as the weight (displacement) of the floating body.
As a
result, the two forces will make up a couple whose moment, ![]() , will be
given by the relation:
, will be
given by the relation:
![]() , (4.23)
, (4.23)
where
![]() (4.24)
(4.24)
is called
metacentric height, and a is the distance on the vertical between the weight
centre and centre of hull; denoting by ![]() and
and ![]() the quotes of these points to a horizontal
reference plane, we shall have:
the quotes of these points to a horizontal
reference plane, we shall have:
![]() (4.25)
(4.25)
The metacentric height, expressed by the relation (4.24) may be positive, negative or nil. We shall in turn analyse each of these cases.
a) if h > 0 the metacentre will be
above the weight centre, and the moment ![]() , given by
the relation (4.24) will also be positive. From fig.4.8.it can be noticed that,
in this case, the moment
, given by
the relation (4.24) will also be positive. From fig.4.8.it can be noticed that,
in this case, the moment ![]() will tend to
return the floating body to the initial floating
will tend to
return the floating body to the initial floating ![]() ; for this
reason it is called restoring moment. In this case the floating of the body
will be stable.
; for this
reason it is called restoring moment. In this case the floating of the body
will be stable.
b) if h < 0, the metacentre is below
the centre of weight (fig.4.9 a). It can be noticed that, in this case, the
moment ![]() will be negative and will slant the floating
body even further. As a result, it will be called moment of force tending to
capsize, the floating of the body being unstable.
will be negative and will slant the floating
body even further. As a result, it will be called moment of force tending to
capsize, the floating of the body being unstable.
c) If h = 0, the metacentre and the centre of hull will superpose (fig.4.9 b). Consequently, the restoring moment will be nil, and the body will float in equilibrium on the slanting floating.
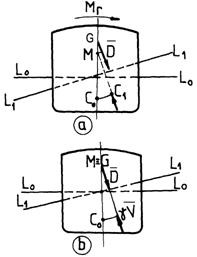
Fig.4.9 a, b
In this case the floating is also unstable. Thus, the stability conditions of the floating are: the metacentre should be placed above the weight centre, namely
![]() (4.26)
(4.26)
According to (4.24) and (4.23), we may write:
![]() (4.27)
(4.27)
where:
![]() , (4.28)
, (4.28)
is called stability moment of form, and:
![]() (4.29)
(4.29)
is called stability moment of weight.
As a result, on the basis of (4.27) we can consider the restoring moment as an algebraic sum of these two moments.
In the case of small longitudinal slantings, the above stated considerations are also valid, the restoring moment being in this case:
![]() (4.30)
(4.30)
where
![]() (4.31)
(4.31)
represents the longitudinal metacentric height, and R is the longitudinal metacentric radius.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2278
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved