| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
A hydrodynamic profile is a contour with an elongated shape with respect to the direction of stream, rounded at the front edge-called leading edge-and having a peak at the back edge, called trailing edge.
 In what follows we shall stress on some of the elements, which
characterise the profile.
In what follows we shall stress on some of the elements, which
characterise the profile.
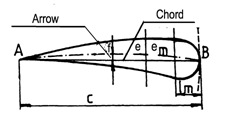
a) The chord of the profile is defined as the straight line which joins the trailing edge A, with the point B, in which the circle
Fig.9.1
with the centre in A is tangent to the leading edge; the length of the chord will be noted by c (fig.9.1).
b) The
thickness of the profile is measured on the normal to the chord and is noted by
e. This thickness varies along the chord and reaches a maximum in a section
which is called section of maximum thickness, situated at the distance ![]() to the leading edge.
to the leading edge.
c) Relative
thickness, ![]() , and
maximum relative thickness,
, and
maximum relative thickness, ![]() , are
defined by the relations:
, are
defined by the relations:
![]() (9.1)
(9.1)
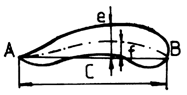
d) The framework of a profile, or the line of mean curvature, is the curve that joins the mean thickness points. The shape of the framework is an important geometric parameter and is linked to the curvature motion of the profile.
From this point of view, profiles can be with simple curvature (fig.9.1) or with double curvature (9.2).
e) The arrow of the profile, f, is the maximum distance, measured on the normal to the chord, between the framework and the chord of the profile.
f)
 The
extrados and intrados of the profile represent the upper and lower part of the
profile, respectively.
The
extrados and intrados of the profile represent the upper and lower part of the
profile, respectively.
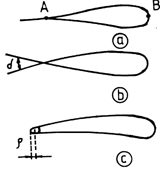
By the geometric shape of the trailing edge, which plays an important part in the theory of profiles, we may distinguish among three categories of profiles:
Fig.9.2
Jukovski profiles, profiles with a sharp edge, for which the tangents to the trailing edge at extrados and intrados superpose (fig.9.3 a)
Karman-Trefftz profiles, or profiles with a dihedral tip, for which the
tangents to the extrados and the intrados
make an angle ![]() in the
in the
trailing edge (fig.9.3 b),
Carafoli profiles, or profiles with the rounded tip, for which the trailing
edge ends in a rounded contour, with a small curvature radius.
(fig.9.3c).
 It is generally studied the plane potential motion around the
hydrodynamic profile, considered as the intersection of the complex plane of
motion with a cylindrical object (called wing), normal on this plane and having
an infinite length (called span).
It is generally studied the plane potential motion around the
hydrodynamic profile, considered as the intersection of the complex plane of
motion with a cylindrical object (called wing), normal on this plane and having
an infinite length (called span).
In reality, wings have a finite span and, from a geometrical point of view, they are characterised by the section of the wing, which, generally, alters
Fig.9.3 a, b, c
the length of the wing and the shape of the wing in plane.
By the shape of the wing in plane, there are: rectangular wings (fig.9.4), trapezoidal wings (9.4 b), elliptical (9.4 c), and triangular wings (9.4 d).
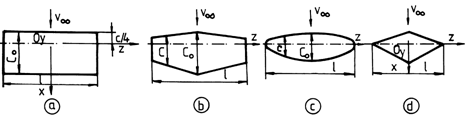
Fig.9.4 a, b, c, d
An important parameter of the wing is the relative elongation defined by the relation:
![]() (9.2)
(9.2)
where l and S represent the span and the surface of the wing, respectively.
In
the particular case of rectangular wing, the length of the chord is constant ![]() and relation (9.2) becomes:
and relation (9.2) becomes:
![]()
since:
![]()
We
can classify wings by their elongation ![]() ; into:
; into:
wings of infinite span, when ![]() ;
;
wings of finite span, when ![]() .
.
Kutta-Jukovskis relation (5.62) can be applied to any solid body in relative displacement with respect to a fluid.
It
indicates that whenever there is a circulation ![]() around a
body, there arises a lift force
around a
body, there arises a lift force ![]() , whose
value is determined, under the same circumstances of environment (
, whose
value is determined, under the same circumstances of environment (![]() ), by the
intensity of circulation.
), by the
intensity of circulation.
To get a higher circulation around bodies, we can act in two ways:
for geometrical symmetric bodies: they are
asymmetrically placed with respect to ![]() direction or a rotational motion is induced
(an infinitely long cylinder, sphere-Magnus effect).
direction or a rotational motion is induced
(an infinitely long cylinder, sphere-Magnus effect).
for asymmetrical bodies: study of shapes more proper to circulation.
On the basis of many theoretical and experimental studies, we have come to designing wings with a high lift, called hydrodynamic profiles.
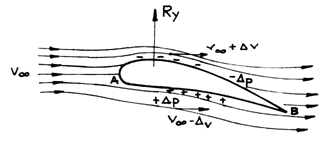
Fig.9.5
In fig.9.5, the arising of circulation around the hydrodynamic profile,
alters the spectre of lines of rectilinear stream, of velocity ![]() as follows: on the extrados the sense of
circulations coincides with that of motion and is seen as a supplement of
velocity
as follows: on the extrados the sense of
circulations coincides with that of motion and is seen as a supplement of
velocity ![]() , and on the
intrados velocity is decreased with
, and on the
intrados velocity is decreased with ![]() .
.
According to Bernoullis law, the velocities asymmetry brings about the static pressures asymmetry (high pressure on the intrados, low pressure on the extrados) as well as the arising of lift force.
Applying
Bernoullis relation between a point at ![]() and a point on the profile, we get:
and a point on the profile, we get:
![]() (9.3)
(9.3)
The pressure coefficient is defined by the relation:
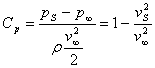 (9.4)
(9.4)
In
fig. 9.6 it is shown the distribution of pressure and of the pressure
coefficient on a hydrodynamic profile at a certain angle of incidence, ![]() .
.
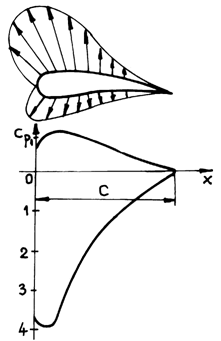
Fig.9.6
The alteration of the incidence angle leads to the shift in the pressures distribution.

The
forces which act upon hydrodynamic or aerodynamic profiles: lift, shape
resistance, friction force or the force due to the detachment of the limit
layer give a resultant ![]() which decomposes by the direction of velocity
in infinite and by a direction which is perpendicular on it (fig.9.7).
Component
which decomposes by the direction of velocity
in infinite and by a direction which is perpendicular on it (fig.9.7).
Component ![]() is called resistance at advancement, and
component
is called resistance at advancement, and
component ![]() , lift force.
, lift force.
They are usually written in the form:
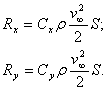 (9.5)
(9.5)
where
![]() is called the coefficient of resistance at
advancement, and
is called the coefficient of resistance at
advancement, and ![]() the lift coefficient (
the lift coefficient (![]() for
profiles of constant chord).
for
profiles of constant chord).
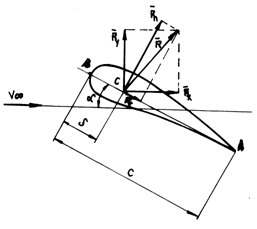
Fig.9.7
Force
![]() can also decompose by the direction of chord
(component
can also decompose by the direction of chord
(component ![]() ) and by a
direction perpendicular on the chord (component
) and by a
direction perpendicular on the chord (component ![]() ).
).
These components may also be expressed with the help of coefficients:
![]() - the coefficient of tangent force and
- the coefficient of tangent force and ![]() - the coefficient of normal force.
- the coefficient of normal force.
For a certain angle ![]() is the distance between the leading edge and
the pressure centre (the application point of hydrodynamic force).
is the distance between the leading edge and
the pressure centre (the application point of hydrodynamic force).
The relation expresses the moment of the force R with respect to the leading edge:
![]() (9.7)
(9.7)
Also, moment M can be expressed by an analytic form similar to that used for the components of hydrodynamic force:
![]() (9.8)
(9.8)
Using (9.5), (9.7), and (9.8), we get:
![]() (9.9)
(9.9)
In the case of small incidence angles:
![]() (9.10)
(9.10)
The
usage of coefficients ![]() ,
, ![]() and
and ![]() is often met in actual practice. Their
variation is studied in different conditions and given in the form of tables
and graphics of great importance for the calculus and design of systems, which
deal with profiles.
is often met in actual practice. Their
variation is studied in different conditions and given in the form of tables
and graphics of great importance for the calculus and design of systems, which
deal with profiles.
Coefficients
![]() ,
, ![]() and
and ![]() depend on the following main elements:
depend on the following main elements:
the shape of the profile;
the span of the profile (finite or infinite, finite of small span or great span);
the type of the flow (Reynolds number);
rugosity of surfaces;
the angle of incidence.
For
each shape of profile, at certain different relative elongation, ![]() , (see
paragraph 9.1), in the case of certain flow velocities (numbers Re variable),
there are diagrams experimentally established
, (see
paragraph 9.1), in the case of certain flow velocities (numbers Re variable),
there are diagrams experimentally established ![]() .
.
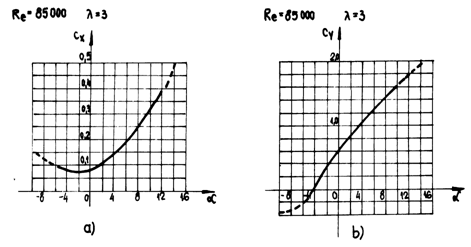
Fig.9.8
In fig. 9.8 there are plotted the diagrams of coefficients for resistance at advancement and for lift force for a NACA 6412 profile, of relative elongation 3, at a number Re = 85,000.
Another
type of diagram often used is the polar profile, namely the function ![]() at different slanting angles (fig.9.9). The polar
allows us to define two characteristics of the profile:
at different slanting angles (fig.9.9). The polar
allows us to define two characteristics of the profile:
the floating or gliding coefficient:
![]() (9.11)
(9.11)
aerodynamic accuracy:
![]() (9.12)
(9.12)
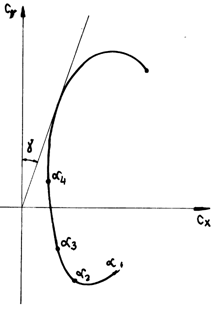
Fig.9.9
For
wings of great span, considered infinite ![]() , the motion
around the profile is plane. Circulation
, the motion
around the profile is plane. Circulation ![]() may be replaced by a whirl.
may be replaced by a whirl.
 In
reality, at the tips of the wing, because of the difference in pressure, there
arises a motion of fluid from intrados to extrados (9.10). The greater the
weight of this motion, the smaller the wing span is.
In
reality, at the tips of the wing, because of the difference in pressure, there
arises a motion of fluid from intrados to extrados (9.10). The greater the
weight of this motion, the smaller the wing span is.
Fig. 9.10
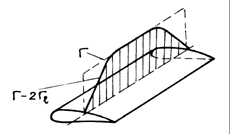 As
a consequence, circulation
As
a consequence, circulation ![]() is no longer constant; at the tips there is a
minimum. (fig.9.11).
is no longer constant; at the tips there is a
minimum. (fig.9.11).
This leads to an alteration of hydrodynamic parameters, through the arising of the so-called induced resistance.
In fig.9.12 the scheme of hydrodynamic forces for the wing of finite span is plotted.
Due
to the arising of an induced velocity ![]() , created by
the free whirl, perpendicular on the velocity in infinite
, created by
the free whirl, perpendicular on the velocity in infinite ![]() , the
resultant velocity becomes:
, the
resultant velocity becomes:
![]() (9.13)
(9.13)
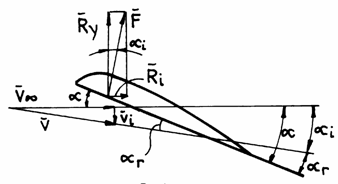
Fig.9.12
As
a consequence there will appear an induced incidence angle ![]() , which thus
decreases the incidence angle
, which thus
decreases the incidence angle ![]() .
.
The alteration of direction and value of velocity bring about the corresponding alteration of lift, which, as we have already shown, is perpendicular on the direction of stream velocity.
If ![]() is the lift of the infinite profile and
is the lift of the infinite profile and ![]() is the lift under the circumstances of an
induced velocity (perpendicular on the direction of velocity
is the lift under the circumstances of an
induced velocity (perpendicular on the direction of velocity ![]() ), then:
), then:
![]() (9.14)
(9.14)
In
the conditions of very small values of ![]() , we may
assume that
, we may
assume that ![]() , namely
lift does not alter.
, namely
lift does not alter.
Component
![]() acting on the direction Ox is called induced
resistance and may be written in the form:
acting on the direction Ox is called induced
resistance and may be written in the form:
![]() (9.15)
(9.15)
The
total resistance of the wing of infinite span is the sum between the resistance
of wing of infinite span ![]() and the induced resistance
and the induced resistance ![]() .
.
Several profiles that are in the stream of fluid are in reciprocal influence, behaving in a different manner within the assembly, rather than solitary. Networks of profiles are often met in practice in the hydraulic or pneumatic units, propellers, etc.
To study the behaviour of profiles in network, let us consider a system made up of several identical profiles, of span l and control contour ABCD (fig.9.13). The pitch of the network is t.
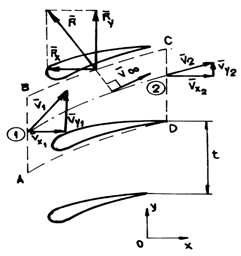
Fig.9.13
Velocities v in points 1 and 2 have the components ![]() and
and ![]() , according
to the system of axes shown in the figure. Assuming that the density of fluid
doesnt alter in a significant way when passing through the network,
, according
to the system of axes shown in the figure. Assuming that the density of fluid
doesnt alter in a significant way when passing through the network, ![]() , then
, then ![]() .
.
Indeed, applying the equation of continuity:
![]() (9.16)
(9.16)
it
results ![]() .
.
We have denoted by m the massic flow. Applying the theorem of impulse,
we get component ![]() of the lift force in the network:
of the lift force in the network:
![]() (9.17)
(9.17)
The circulation of velocity on the control contour will be:
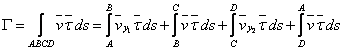 (9.18)
(9.18)
The integrals on the segments of contour BC and AD cancel reciprocally. There only remains:
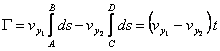 (9.19)
(9.19)
Therefore:
![]() (9.20)
(9.20)
Replacing (9.20) into (9.17), we get:
![]() (9.21)
(9.21)
The axial component ![]() is due to the difference of pressure:
is due to the difference of pressure:
![]() (9.22)
(9.22)
Applying Bernoullis equation between the points 1 and 2, we get:
![]() (9.23)
(9.23)
or else:
![]() (9.24)
(9.24)
Replacing (9.24) into (9.22). we get:
![]() (9.25)
(9.25)
The resultant force will be:
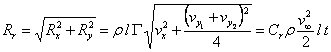 (9.26)
(9.26)
In relation (9.26) we have denoted by ![]() the coefficient of the network and by
the coefficient of the network and by ![]() the mean velocity in the network (fig.9.14).
the mean velocity in the network (fig.9.14).
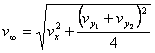 (9.24)
(9.24)
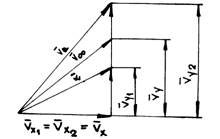
Fig.9.14
The
lift force is perpendicular on ![]() .
Coefficient
.
Coefficient ![]() is different from the hydro-aerodynamic
coefficient corresponding to a separate profile.
is different from the hydro-aerodynamic
coefficient corresponding to a separate profile.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2608
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved