| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
The motion of real fluids can be carried out under two regimes of different quality: laminar and turbulent.
These motion regimes were first emphasised by the English physicist in
mechanics Osborne Reynolds in 1882, who made systematic experimental studies
concerning the flow of water through glass conduits of diameter ![]() .
.
The experimental installation, which was then used, is schematically shown in fig.7.1.
Fig.7.1
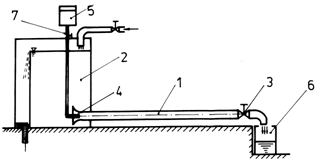
The transparent conduit 1, with a very accurate processed inlet, is supplied by tank 2, full of water, at a constant level.
The flow that passes the transparent conduit can be adjusted by means of tap 3, and measured with the help of graded pot 6.
In conduit 1, inside the water stream we insert, by means of a thin tube 4, a coloured liquid of the same density as water. The flow of coloured liquid, supplied by tank 5 may be adjusted by means of tap 7.
But slightly turning on tap 3, through conduit 1 a stream of water will pass at a certain flow and velocity.
If we turn on tap 7 as well, the coloured liquid inserted through the thin tube 4, engages itself in the flow in the shape of a rectilinear thread, parallel to the walls of conduit, leaving the impression that a straight line has been drawn inside the transparent conduit 1.
This regime of motion under which the fluid flows in threads that dont mix is called a laminar regime.
By slowly continuing to turn on tap 3, we can notice that for a certain flow velocity of water, the thread of liquid begins to undulate, and for higher velocities it begins to pulsate, which shows that vector velocity registers variations in time (pulsations).
For even higher velocities, the pulsations of the coloured thread of water increase their amplitude and, at a certain moment, it will tear, the particles of coloured liquid mixing with the mass of water that is flowing through conduit 1.
The regime of motion in which, due to pulsations of velocity, the particles of fluid mix is called a turbulent regime.
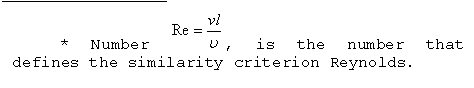 The
shift from a laminar regime to the turbulent one, called a transition regime is
characterised by a certain value of Reynolds number
The
shift from a laminar regime to the turbulent one, called a transition regime is
characterised by a certain value of Reynolds number![]() , called
critical value (
, called
critical value (![]() ).
).
For circular smooth conduits, the critical value of Reynolds number is ![]() .
.
For values of Reynolds number inferior to the critical value (![]() ), the
motion of liquid will be laminar, while for
), the
motion of liquid will be laminar, while for ![]() , the flow
regime will be turbulent.
, the flow
regime will be turbulent.
Navier Stokes equation describes the motion of real (viscous) incompressible fluids in a laminar regime.
Unlike ideal fluids that are capable to develop only unitary compression efforts that are exclusively due to their pressure, real (viscous) fluids can develop normal or tangent supplementary viscosity efforts.
The expression of the tangent viscosity effort, defined by Newton (see chapter 2) is the following:
![]() (7.1)
(7.1)
Newtonian liquids are capable to develop, under a laminar regime,
viscosity efforts ![]() and
and ![]() , that
make-up the so-called tensor of the viscosity efforts,
, that
make-up the so-called tensor of the viscosity efforts, ![]() (in fig. 7.2, efforts manifest on an
elementary parallelipipedic volume of fluid with the sides
(in fig. 7.2, efforts manifest on an
elementary parallelipipedic volume of fluid with the sides ![]() ):
):
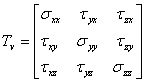 (7.2)
(7.2)
The tensor ![]() is symmetrical:
is symmetrical:
![]() (7.3)
(7.3)
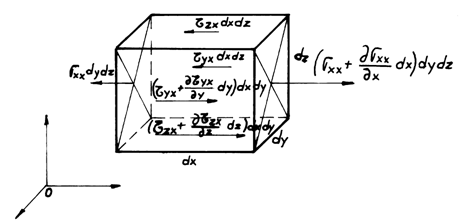
Fig.7.2
The elementary force of viscosity that is exerted upon the elementary volume of fluid in the direction of axis Ox is:
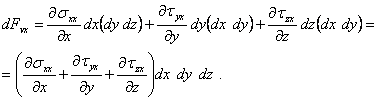 (7.4)
(7.4)
According to the theory of elasticity:
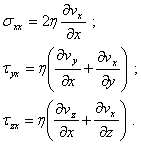 (7.5)
(7.5)
Thus:
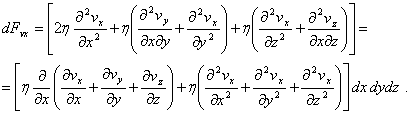
But ![]() , according
to the equation of continuity for liquids.
, according
to the equation of continuity for liquids.
Then:
![]() (7.7)
(7.7)
Similarly:
![]() (7.8)
(7.8)
![]() (7.9)
(7.9)
Hence:
![]() (7.10)
(7.10)
![]() (7.11)
(7.11)
Unlike the ideal fluids, in dAlemberts principle the viscosity force also appears.
![]() (7.12)
(7.12)
Introducing relations (3.3), (3.5), (3.7) and (7.11) into (7.12), we get:
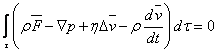 (7.13)
(7.13)
or:
![]() (7.14)
(7.14)
Relation (7.14) is the vectorial form of Navier-Stokes equation. The scalar form of this equation is:
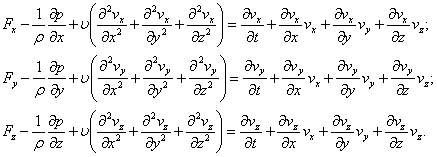 (7.15)
(7.15)
Unlike the permanent motion of an ideal fluid, where its specific energy![]() remains
constant along the thread of fluid and where, from one section to another,
there takes place only the conversion of a part from the potential energy into
kinetic energy, or the other way round, in permanent motion of the real fluid,
its specific energy is no longer constant. It always decreases in the sense of
the movement of the fluid.
remains
constant along the thread of fluid and where, from one section to another,
there takes place only the conversion of a part from the potential energy into
kinetic energy, or the other way round, in permanent motion of the real fluid,
its specific energy is no longer constant. It always decreases in the sense of
the movement of the fluid.
A part of the fluids energy is converted into thermal energy, is irreversibly spent to overcome the resistance brought about by its viscosity.
Denoting this specific energy (load) by ![]() ,
Bernoullis equation becomes:
,
Bernoullis equation becomes:
![]() (7.16)
(7.16)
![]() In
different points of the same section, only the potential energy remains
constant, the kinetic one is different since the velocity differs in the
section,
In
different points of the same section, only the potential energy remains
constant, the kinetic one is different since the velocity differs in the
section, ![]() . In this
case the term of the kinetic energy should be corrected by a coefficient
. In this
case the term of the kinetic energy should be corrected by a coefficient ![]() , that
considers the distribution of velocities in the section
, that
considers the distribution of velocities in the section ![]() .
.
![]() (7.17)
(7.17)
By reporting the loss of load ![]() to the length l of a straight conduit, we get
the hydraulic slope (fig.7.3):
to the length l of a straight conduit, we get
the hydraulic slope (fig.7.3):
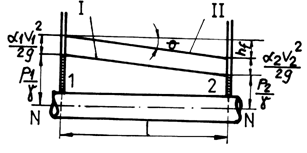
Fig.7.3
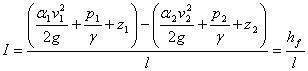 . (7.18)
. (7.18)
If we refer only to the potential specific energy, we get the piezometric slope:
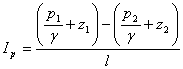 (7.19)
(7.19)
In the case of uniform motion (![]() ):
):
![]() (7.20)
(7.20)
Experimental researches have revealed that irrespective of the regime under which the motion of fluid takes place, the losses of load can be written in the form:
![]() (7.21)
(7.21)
where b is a coefficient that considers the nature of the fluid, the dimensions of the conduit and the state of its wall.
![]() for laminar regime;
for laminar regime;
![]() for turbulent regime.
for turbulent regime.
If we logarithm (7.21) we get:
![]() (7.22)
(7.22)
In
fig. 7.4 the load variation ![]() with respect to velocity is plotted in
logarithmic co-ordinates.
with respect to velocity is plotted in
logarithmic co-ordinates.
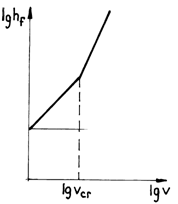
Fig.7.4
For the laminar regime ![]() . The shift
to the turbulent regime is made for a velocity corresponding to
. The shift
to the turbulent regime is made for a velocity corresponding to ![]() .
.
To determine the velocity distribution between two plane parallel boards of infinite length, we shall integrate the equation (7.15) under the following conditions:
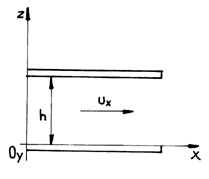
Fig.7.5
a) velocity has only the direction of the axis Ox:
![]() (7.23)
(7.23)
from
the equation of continuity ![]() , it
results:
, it
results:
![]() (7.24)
(7.24)
therefore velocity does not vary along the axis Ox.
b) the movement is identically reproduced in planes parallel to xOz:
![]() (7.25)
(7.25)
From
(7.24) and (7.25) it results that ![]() .
.
c) the motion is permanent:
![]() (7.26)
(7.26)
d) we leave out the massic forces (the horizontal conduit).
e) the fluid is incompressible.
The first equation (7.15) becomes:
![]() (7.27)
(7.27)
Integrating twice (7.27):
![]() (7.28)
(7.28)
For the case of fixed boards, we have the conditions at limit:
![]() (7.29)
(7.29)
Subsequently:
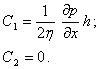 (7.30)
(7.30)
Then the law of velocity distribution will be:
![]() (7.31)
(7.31)
It
is noticed that the velocity distribution is parabolic, having a maximum for ![]() :
:
![]()
![]() (7.32)
(7.32)
Computing the mean velocity in the section:
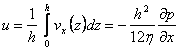 (7.33)
(7.33)

well
notice that ![]() .
.
The flow that passes through a section of breadth b will be:
![]() (7.34)
(7.34)
Lets
consider a circular conduit, of radius ![]() and length l, through which an incompressible
fluid of density
and length l, through which an incompressible
fluid of density ![]() and kinematic viscosity
and kinematic viscosity ![]() (fig.7.6) passes.
(fig.7.6) passes.
We
report the conduit to a system of cylindrical co-ordinates (![]() ), the axis
Ox, being the axis of the conduit. The movement being carried out on the
direction of the axis, the velocity components will be:
), the axis
Ox, being the axis of the conduit. The movement being carried out on the
direction of the axis, the velocity components will be:
![]() (7.35)
(7.35)
The
equation of continuity ![]() , written in
cylindrical co-ordinates:
, written in
cylindrical co-ordinates:
![]() (7.36)
(7.36)
becomes:
![]() (7.37)
(7.37)
where from we infer that the velocity of the fluid doesnt vary on the length of the conduit.
On the other hand, taking into consideration the axial symmetrical
character of the motion, velocity will neither depend on variable ![]() .
.
As a result, for a permanent motion, it will only depend on variable r,
that is ![]() .
.
The distribution of velocities in the section of flow can be obtained by integrating the Navier-Stokes equations (7.14).
Noting by ![]() and
and ![]() the versors of the three directions of the
adopted system of cylindrical co-ordinates, we can write vector velocity:
the versors of the three directions of the
adopted system of cylindrical co-ordinates, we can write vector velocity:
![]() (7.38)
(7.38)
Bearing in mind that in cylindrical co-ordinates, operator ![]() has the expression:
has the expression:
![]() (7.39)
(7.39)
On the basis of (7.38), we can write:
![]() (7.40)
(7.40)
since,
as we have seen, velocity ![]() only depends on variable r.
only depends on variable r.
On
the other hand, in cylindrical co-ordinates, the term ![]() may be rendered in the form:
may be rendered in the form:
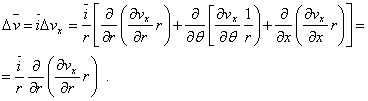 (7.41)
(7.41)
Keeping in mind the permanent character of the motion, relation (7.40) and (7.41) the projection of equation (7.14) onto the axis Ox may be written in the form:
![]() (7.42)
(7.42)
since,
on the hypothesis of a horizontal conduit, ![]() .
.
Assuming that the gradient of pressure on the direction of axis Ox is
constant (![]() ), and
integrating the equation (7.42), we shall successively get:
), and
integrating the equation (7.42), we shall successively get:
![]() (7.43)
(7.43)
![]() (7.44)
(7.44)
The integrating constants ![]() and
and ![]() are determined using the limit conditions:
are determined using the limit conditions:
in the axis of conduit, at r = 0, velocity
should be finite, thus constant ![]() should be nil;
should be nil;
on the wall of conduit, at ![]() , velocity
of fluid should be nil; consequently:
, velocity
of fluid should be nil; consequently:
![]() (7.45)
(7.45)
and relation (7.44) becomes:
![]() (7.46)
(7.46)
From (7.46) we notice that if the motion takes place in the positive
sense of the axis ![]() , then
, then ![]() ; therefore
pressure decreases on the direction of motion if I is the piezometric slope
(equal in this case to the hydraulic slope), we can write:
; therefore
pressure decreases on the direction of motion if I is the piezometric slope
(equal in this case to the hydraulic slope), we can write:
![]() (7.47)
(7.47)
where
![]() is the fall of pressure on the length l of the
conduit. Subsequently, relation (7.41) becomes:
is the fall of pressure on the length l of the
conduit. Subsequently, relation (7.41) becomes:
![]() (7.48)
(7.48)
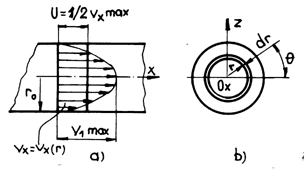
Fig.7.6
It can be noticed that the distribution of velocities in the section of flow is parabolic (fig.7.6 a), the maximum velocity being registered in the axis of conduit (r = 0), therefore we get:
![]() (7.49)
(7.49)
Let us now consider an elementary surface d A in the shape of a circular crown of radius r and breadth d r (fig.7.6 b). The elementary flow that crosses surface d A is:
![]() (7.50)
(7.50)
and:
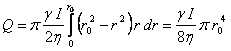 (7.51)
(7.51)
The mean velocity has the expression:
![]() (7.52)
(7.52)
Further on we can write:
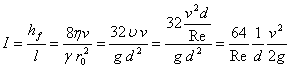 (7.53)
(7.53)
Relation (7.53) is Hagen-Ppiseuilles law, which gives us the value of load linear losses in the conduits for the laminar motion:
![]() (7.54)
(7.54)
![]() is the hydraulic resistance coefficient for
laminar motion.
is the hydraulic resistance coefficient for
laminar motion.
In a point of the turbulent stream, the fluid velocity registered rapid variation, in one sense or the other, with respect to the mean velocity in section. The field of velocities has a complex structure, still unknown, being the object of numerous studies.
The variation of velocity with the time may be plotted as in fig.7.7.
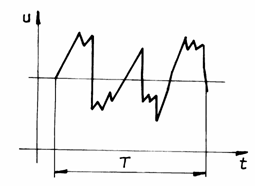
Fig.7.7
A particular case of turbulent motion is the quasipermanent motion (stationary on average). In this case, velocity, although varies in time, remains a constant means value.
In the turbulent motion we define the following velocities:
a)
instantaneous velocity ![]() ;
;
b) mean velocity
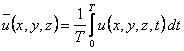 (7.55)
(7.55)
c) pulsation velocity
![]() (7.56)
(7.56)
There are several theories that by simplifying describe the turbulent motion:
a) Theory of mixing length (Prandtl), which admits that the impulse is kept constant.
b) Theory of whirl transports (Taylor) where the rotor of velocity is presumed constant.
c) Karamans theory of turbulence, which states that, except for the immediate vicinity of a wall, the mechanism of turbulence is independent from viscosity.
Determination of load losses in the turbulent motion is an important problem in practice.
It had been experimentally established that in turbulent motion the
pressure loss ![]() depends on the following factors: mean
velocity on section, v , diameter of conduit, d , density
depends on the following factors: mean
velocity on section, v , diameter of conduit, d , density ![]() of the fluid and its kinematic viscosity
of the fluid and its kinematic viscosity ![]() , length l
of the conduit and the absolute rugosity
, length l
of the conduit and the absolute rugosity ![]() of its interior walls; therefore:
of its interior walls; therefore:
![]() (7.57)
(7.57)
or:
![]() (7.58)
(7.58)
![]() (7.59)
(7.59)

![]() - relative rugosity
- relative rugosity
where:
![]() (7.60)
(7.60)
As it can be seen from relation (7.60), in turbulent motion the
coefficient of load loss ![]() may depend either on Reynolds number or on the
relative rugosity of the conduit walls.
may depend either on Reynolds number or on the
relative rugosity of the conduit walls.
In its turbulent flow through the conduit, the fluid has a turbulent core, in which the process of mixing is decisive in report to the influence of viscosity and a laminar sub-layer, situated near the wall, in which the viscosity forces have a decisive role.
If
we note by ![]() the thickness of the laminar sub-layer, then
we can classify conduits as follows:
the thickness of the laminar sub-layer, then
we can classify conduits as follows:
conduits with smooth walls; ![]() ;
;
conduits with rugous walls; ![]() .
.
From
(7.60) we notice that, unlike the laminar motion in turbulent motion ![]() is a complex function of
is a complex function of ![]() and
and ![]() .
.
It
has been experimentally established that in the case of hydraulic smooth
conduits, coefficient ![]() depends only on Reynolds number. Thus,
Blasius, by processing the existent experimental material (in 1911),
established for the smooth hydraulic conduits of circular section, the
following empirical formula:
depends only on Reynolds number. Thus,
Blasius, by processing the existent experimental material (in 1911),
established for the smooth hydraulic conduits of circular section, the
following empirical formula:
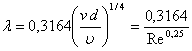 (7.61)
(7.61)
valid
for ![]() .
.
Using Blasius relation in (7.59) we notice that under this motion regime the load losses are proportional to velocity to 1,75th power.
Also for smooth conduits, but for higher Reynolds numbers ![]() we can use Konakovs relation:
we can use Konakovs relation:
![]() (7.62)
(7.62)
In turbulent flow through conduits, coefficient ![]() no longer depends on Reynolds number, and it
can be determined with the help of Prandtl Nikuradses relation:
no longer depends on Reynolds number, and it
can be determined with the help of Prandtl Nikuradses relation:
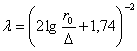 (7.63)
(7.63)
Some
of the most important formulae for the calculus of coefficient ![]() are given in table 7.1, the validity field of
each relation being also shown [7].
are given in table 7.1, the validity field of
each relation being also shown [7].
Table 7.1
|
No. |
aI |
Relation |
Regime |
Field |
|||
|
I |
|
III |
IV |
V |
|||
|
Poisseuille |
|
Laminar |
|
||||
|
Prandtl |
|
Smooth turbulent |
|
||||
|
Blasius |
|
|
|||||
|
Konakov |
|
|
|||||
|
Nikuradze |
|
|
|||||
|
|
Lees |
|
|
||||
|
Colebrook-White |
|
Demi-rugous |
Universal |
||||
|
Prandtl-Nikurdze |
|
Turbulent rugous |
|
||||
|
Sifrinson |
|
|
On
the basis of experiments made with conduits of homogeneous different rugosity,
which was achieved by sticking on the interior wall some grains of sand of the
same diameter, Nikuradze has made up a diagram that represents the way coefficient ![]() varies, both
for laminar and turbulent fields (fig.7.8).
varies, both
for laminar and turbulent fields (fig.7.8).
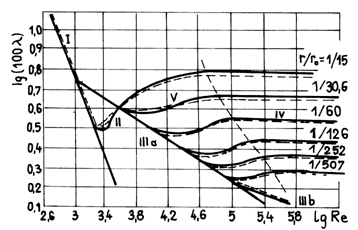
Fig.7.8
We
can notice that in the diagram appear five areas in which variation of
coefficient ![]() , distinctly
differs.
, distinctly
differs.
Area I is a straight line which represents in logarithmic co-ordinates the variation:
![]() (7.64)
(7.64)
corresponding to the laminar
regime ![]() . On this
line all the doted curves are superposed, which represents variation
. On this
line all the doted curves are superposed, which represents variation ![]() for different relative rugosities
for different relative rugosities ![]() .
.
Area II is the shift from laminar regime to the
turbulent one which takes place for ![]() .
.
Area III corresponds to the smooth hydraulic conduits.
In this area coefficient ![]() can be determined with the help of Blasius
relation (7.61), to which the straight line III a corresponds, called Blasius
straight. Since the validity field of relation (7.61) is limited by
can be determined with the help of Blasius
relation (7.61), to which the straight line III a corresponds, called Blasius
straight. Since the validity field of relation (7.61) is limited by ![]() , for higher
values of Reynolds number, we use Kanakovs formula, to which curve III b
corresponds. It is noticed that the smaller the relative rugosity is, the
greater the variation field of Reynolds number, in which the smooth turbulent
regime is maintained.
, for higher
values of Reynolds number, we use Kanakovs formula, to which curve III b
corresponds. It is noticed that the smaller the relative rugosity is, the
greater the variation field of Reynolds number, in which the smooth turbulent
regime is maintained.
In area IV each discontinuous curve,
which represents dependent ![]() for different relative rugosities becomes
horizontal, which emphasises the independence of
for different relative rugosities becomes
horizontal, which emphasises the independence of ![]() on number
on number ![]() . Therefore
this area corresponds to the rugous turbulent regime, where
. Therefore
this area corresponds to the rugous turbulent regime, where ![]() is determined by (7.63).
is determined by (7.63).
It is noticed that in this case the losses of load (7.59) are proportional to square velocity.
For this reason the rugous turbulent regime is also called square regime.
Area V is characterised by the dependence of the coefficient both on Reynolds number and on the relative rugosity of the conduit.
It
can be noticed that for areas IV and V, coefficient ![]() decreases with the decrease of relative
rugosity.
decreases with the decrease of relative
rugosity.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3125
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved