| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
The potential motion is characterised by the fact that the whirl vector is nil.
![]() (5.1)
(5.1)
hence its name: irrotational.
If ![]() is nil, its components on the three axes will
also be nil:
is nil, its components on the three axes will
also be nil:
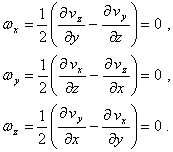 (5.2)
(5.2)
or:
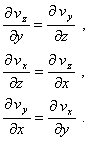 (5.3)
(5.3)
Relations
(5.3) are satisfied only if velocity v derives from a function ![]() :
:
![]() (5.4)
(5.4)
or vectorially:
![]() (5.5)
(5.5)
Indeed:
![]() (5.6)
(5.6)
Function ![]() is called the potential of velocities.
is called the potential of velocities.
If we apply the equation of continuity for liquids,
![]() (5.7)
(5.7)
we shall
notice that function ![]() verifies equation of
verifies equation of
![]() (5.8)
(5.8)
thus being a harmonic function.
The motion of the fluid is called plane or bidimensional if all the particles that are found on the same perpendicular at an immobile plane, called director plane, move parallel with this plane, with equal velocities.
If the
director plane coincides with xOy, then ![]() .
.
A plane
motion becomes unidimensional if components ![]() and
and ![]() of the velocity of the fluid depend only on a
spatial co-ordinate.
of the velocity of the fluid depend only on a
spatial co-ordinate.
For plane motion, the equation of the streamline will be:
![]() (5.9)
(5.9)
or else:
![]() (5.10)
(5.10)
and the equation of continuity:
![]() (5.11)
(5.11)
The left
term of the equation (5.10) is an exact total differential of function ![]() , called the
stream function:
, called the
stream function:
![]() (5.12)
(5.12)
![]() (5.13)
(5.13)
Function ![]() verifies the equation of continuity (5.11):
verifies the equation of continuity (5.11):
![]() (5.14)
(5.14)
Function ![]() is a harmonic one as well:
is a harmonic one as well:
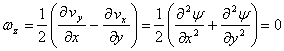 (5.15)
(5.15)
![]() (5.16)
(5.16)
The total
of the points, in which the potential function ![]() is constant,
define the equipotential surfaces.
is constant,
define the equipotential surfaces.
In the case of a potential plane motion:
![]() - constant, equipotential lines of velocity;
- constant, equipotential lines of velocity;
![]() - constant, stream lines.
- constant, stream lines.
Computing the circulation of velocity along a certain outline, in the mass of fluid, between points A and B (fig.5.1), we get:
![]() (5.17)
(5.17)
Thus, the circulation of velocity
doesnt depend on the shape of the curve AB, but only on the values of the
function ![]() in A and B. The circulation of velocity is nil
along an equipotential line of velocity (
in A and B. The circulation of velocity is nil
along an equipotential line of velocity (![]() ).
).
If we compute the flow of liquid through the curve AB in the plane motion (in fact through the cylindrical surface with an outline AB and unitary breadth), we get (fig.5.1):
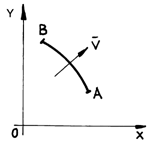
Fig.5.1
![]() (5.18)
(5.18)
Thus, the flow that crosses a curve
does not depend on its shape, but only on the values of function ![]() in the
extreme points. The flow through a streamline is nil
in the
extreme points. The flow through a streamline is nil ![]() .
.
A streamline crosses orthogonal on
an equipotential line of velocity. To demonstrate this propriety we shall take
into consideration that the gradient of a scalar function F is normal on the
level surface F = cons. As a result, vectors ![]() and
and ![]() are normal on the streamlines and on the
equipotential lines of velocity.
are normal on the streamlines and on the
equipotential lines of velocity.
Computing their scalar product, we get:
![]() (5.19)
(5.19)
Since their scalar product is nil, it follows that they are perpendicular, therefore their streamlines are perpendicular on the lines of velocity.
Going back to the expressions of ![]() and
and ![]() :
:
 (5.20)
(5.20)
Relations (5.20) represent the Cauchy-Riemanns monogenic conditions for a function of complex variable.
Any potential plane motion may always be plotted by means of an analytic function of complex variable,
![]()
The analytic function;
![]() (5.21)
(5.21)
is called the complex potential of the plane potential motion.
Deriving (5.21) we get the complex velocity:
![]() (5.22)
(5.22)
Fig.5.2
![]() (5.23)
(5.23)
Having found the complex potential, lets establish a few types of plane potential motions.
Lets consider the complex potential:
![]() (5.24)
(5.24)
where a is a complex constant in the form of:
![]() (5.25)
(5.25)
with ![]() and
and ![]() real and constant positive.
real and constant positive.
Relation (5.24) can be written in the form:
![]() (5.26)
(5.26)
where from
we can get the expressions of functions ![]() and
and ![]() :
:
![]() (5.27)
(5.27)
By equalling these relations with constants we obtain the equations of equipotential lines and of streamlines.
![]() (5.28)
(5.28)
From these equations we notice that the streamlines and equipotential lines are straight, having constant slopes (fig.5.3).
Fig.5.3
 (5.29)
(5.29)
We can easily check the orthogonality of the stream and equipotential lines by writing:
![]() (5.30)
(5.30)
Deriving the complex potential we get the complex velocity:
![]() (5.31)
(5.31)
that enables us to determine the components of velocity in a certain point:
![]() (5.32)
(5.32)
The vector velocity will have the modulus:
![]() (5.33)
(5.33)
and will
have with axis Ox, the angle ![]() , given by
the relation (5.29).
, given by
the relation (5.29).
We can
conclude that the potential vector (5.25) is a rectilinear and uniform flow on
a direction of angle ![]() with the abscissa axis.
with the abscissa axis.
The components of velocity can be also obtained from relations (5.20):
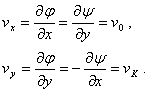 (5.34)
(5.34)
If we
particularise (5.25), by assuming ![]() , the
potential (5.24) will take the form:
, the
potential (5.24) will take the form:
![]() (5.35)
(5.35)
that represents a rectilinear and uniform motion on the direction of the axis Ox.
Analogically,
assuming in (5.25) ![]() , we get:
, we get:
![]() (5.36)
(5.36)
that is the
potential vector of a rectilinear and uniform flow, of velocity ![]() , on the
direction of the axis Oy.
, on the
direction of the axis Oy.
The motion described above will have a reverse sense if the corresponding expressions of the potential vector are taken with a reverse sign.
Lets consider the complex potential:
![]() (5.37)
(5.37)
where Q is a real and positive constant.
Writing the
variable ![]() , this
complex potential becomes:
, this
complex potential becomes:
![]() (5.38)
(5.38)
where
from we get function ![]() and
and ![]() :
:
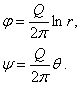 (5.39)
(5.39)
which, equalled with constants, give us the equations of equipotential and stream lines, in the form:
![]() (5.40)
(5.40)
It can be noticed that the equipotential lines are concentric circles with the centre in the origin of the axes, and the streamlines are concurrent lines in this point (fig.5.4).
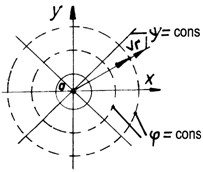
Fig.5.4
Knowing that:
![]() (5.41)
(5.41)
in a point ![]() , the
components of velocity will be:
, the
components of velocity will be:
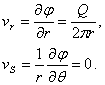 (5.42)
(5.42)
It can noticed that on the circle of radius r = cons., the fluid velocity has a constant modulus, being co-linear with the vector radius of the considered point.
Such a plane potential motion in which the flow takes place radially, in such a manner that along a circle of given radius velocity is constant as a modulus, is called a plane source.
Constant Q, which appears in the above - written relations, is called the flow of the source.
The flow of the source through a circular surface of radius r and unitary breadth will be:
![]() (5.43)
(5.43)
Analogically, the complex potential of the form:
![]() (5.44)
(5.44)
will represent a suction or a well because, in this case, the sense of the velocity is reversing, the fluid moving from the exterior to the origin (where it is being sucked).
If the
source isnt placed in the origin of the axes, but in a point ![]() , of the
real axis, of abscissa
, of the
real axis, of abscissa ![]() , then:
, then:
![]() (5.45)
(5.45)
Let the complex potential be:
![]() (5.46)
(5.46)
where ![]() is a positive and real constant, equal to the
circulation of velocity along a closed outline, which surrounds the origin.
is a positive and real constant, equal to the
circulation of velocity along a closed outline, which surrounds the origin.
Proceeding in the same manner as for
the previous case, we shall get the functions ![]() and
and ![]() :
:
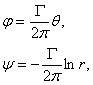 (5.47)
(5.47)
from which
we can notice that the equipotential lines, of equation ![]() are concurrent lines, in the origin of axes,
and the streamlines, having the equation
are concurrent lines, in the origin of axes,
and the streamlines, having the equation ![]() , are
concentric circles with their centre in the origin of the axes (fig.5.5).
, are
concentric circles with their centre in the origin of the axes (fig.5.5).
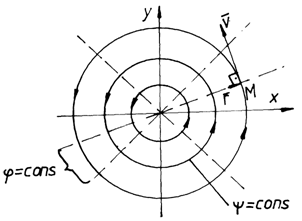
Fig.5.5
The components of velocity are:
![]() (5.48)
(5.48)
Thus, on a circle of given radius r, the velocity is constant as a modulus, has the direction of the tangent to this circle in the considered point and is directed in the sense of angle increase.
If the whirl is placed on the real
axis, in a point with abscissa ![]() , the
complex potential of the motion will be:
, the
complex potential of the motion will be:
![]() (5.49)
(5.49)
The flow
with circulation around a circular cylinder is a plane potential motion that
consists of an axial stream (directed along axis Ox), a dipole of moment ![]() (with a
source at the left of suction) and a whirl (in direct trigonometric sense).
(with a
source at the left of suction) and a whirl (in direct trigonometric sense).
The complex potential of motion will be:
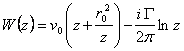 (5.50)
(5.50)
where we have done the denotation:
![]() (5.51)
(5.51)
By writing
the complex variable ![]() , we shall
divide in (5.50) the real part from the imaginary one, thus obtaining functions
, we shall
divide in (5.50) the real part from the imaginary one, thus obtaining functions
![]() and
and ![]() :
:
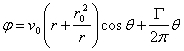 (5.52)
(5.52)
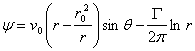 (5.53)
(5.53)

The stream and equipotential lines are obtained by taking in relations (5.52),
(5.53), ![]() respectively. We notice that if in (5.53) we
assume
respectively. We notice that if in (5.53) we
assume ![]() , function
, function ![]() will become constant; therefore we can infer
that the circle of radius
will become constant; therefore we can infer
that the circle of radius ![]() with the centre in the origin of the axes is a
streamline (fig.5.8).
with the centre in the origin of the axes is a
streamline (fig.5.8).
Admitting that this streamline is a
solid border, well be able to consider this motion described by the complex
potential (5.50) as being the flow around a straight circular cylinder of radius
![]() , having the
breadth normal on the motion plane, infinite.
, having the
breadth normal on the motion plane, infinite.
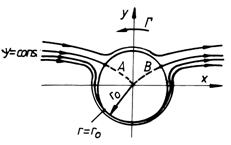 If we plot the other streamlines we
shall get some asymmetric curves with respect to axis Ox (fig.5.6). On the
inferior side of the circle of radius
If we plot the other streamlines we
shall get some asymmetric curves with respect to axis Ox (fig.5.6). On the
inferior side of the circle of radius ![]() , the
velocity due to the axial stream is summed up with the velocity due to the
whirl.
, the
velocity due to the axial stream is summed up with the velocity due to the
whirl.
Fig.5.6
As a result, here we shall obtain smaller velocities, and the streamlines will be more rare.
In
polar co-ordinates, the components of velocity in a certain point ![]() , will be:
, will be:
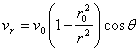 (5.54)
(5.54)
If
the considered point is placed on the circle of radius ![]() , well
have:
, well
have:
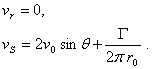 (5.55)
(5.55)
The position of stagnant points can be determined provided that between these points the velocity of the fluid should be nil.
The
flow without circulation around a circular cylinder is the plane potential
motion made up of an axial stream (directed along axis Ox) and a dipole of
moment ![]() (whose source is at the left of suction).
(whose source is at the left of suction).
Thus, this motion can be obtained particularising the motion previously described by cancelling the whirl.
By
making ![]() , in
relations (5.50), (5.52) and (5.53) we get the complex potential of the motion,
the function potential of velocity and the function of stream, in the form:
, in
relations (5.50), (5.52) and (5.53) we get the complex potential of the motion,
the function potential of velocity and the function of stream, in the form:
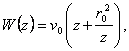 (5.56)
(5.56)
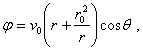 (5.57)
(5.57)
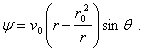 (5.58)
(5.58)
By
writing the equation of streamlines ![]() = cons. in
the form:
= cons. in
the form:
![]() (5.59)
(5.59)
we
notice that the nil streamline (C = 0) is made up of a part of the real axis
(Ox) and the circle of radius ![]() (fig.5.7).
(fig.5.7).
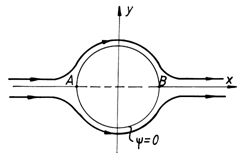 The
other streamlines are symmetric curves with respect to axis Ox. Obviously, if
we consider the circle of radius
The
other streamlines are symmetric curves with respect to axis Ox. Obviously, if
we consider the circle of radius ![]() , as a solid
border, the motion can be seen as a flow of an axial stream around an
infinitely long cylinder, normal on the motion plane.
, as a solid
border, the motion can be seen as a flow of an axial stream around an
infinitely long cylinder, normal on the motion plane.
Fig.5.7
The components of velocity are:
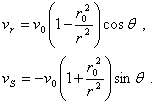 (5.60)
(5.60)
which,
on the circle of radius ![]() , become:
, become:
![]() (5.61)
(5.61)
The position of stagnant points is obtained by making ![]() , which
implies
, which
implies ![]() . Thus the stagnant
points are found on the axis Ox in the points
. Thus the stagnant
points are found on the axis Ox in the points ![]() and
and ![]() .
.
Let us consider a cylindrical body normal on the complex plane, the outline C being the crossing curve between the cylinder and the complex plane.
Around
this outline there flows a stream, potential plane, having the complex
potential ![]() . The
velocity in infinite of the stream, directed in the negative sense of the axis
Ox, is
. The
velocity in infinite of the stream, directed in the negative sense of the axis
Ox, is ![]() .
.
In this case the resultant of the pressure forces will have the components:
![]() (5.62)
(5.62)
The forces are given with respect to the unit of length of the body.
The second relation (5.62) is the mathematic expression of Kutta-Jukovskis theorem, which will be only stated below without demonstrating it:
If a fluid of density ![]() is draining around a body of circulation
is draining around a body of circulation ![]() and velocity in infinite
and velocity in infinite ![]() , it will
act upon the unit of length of the body with a force equal to the product
, it will
act upon the unit of length of the body with a force equal to the product ![]() , normal on
the direction of velocity in infinite called lift force (lift).
, normal on
the direction of velocity in infinite called lift force (lift).
The
sense of the lift is obtained by rotating the vector of velocity from infinite
with ![]() in the reverse sense of circulation.
in the reverse sense of circulation.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1657
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved