THERMAL CONSIDERATIONS

When a transistor (a semiconductor device) supplying the desired current has a voltage across it, it dissipates power in the form of heat. The heat is generated at its junction (wafer) and must flow through its package (casing) to the surrounding air. First of all the heat has to flow from the junction inside the transistor package to its outer surface. The transistor package offers some opposition to the heat flow. We label it as the thermal resistance from the junction-to-case q_JC). When the case temperature is higher than its surrounding medium (air) and there is nothing else involved in the heat-transfer process, then the thermal gradient forces the heat to flow from the case to the surrounding air. The thermal resistance introduced during this process by the heat flow from the case-to-air is labeled as q_CA In fact, the manufacturer of the device provides the total thermal resistance from the junction-to-air as q_JA. As you may have realized that

q_JA q_JC + q_CA

If the ambient temperature (T_A) and the power dissipation by the transistor (P_D) are known, we compute the junction temperature (T_J) as

(11.1)

The manufacturer usually specifies the maximum junction temperature. If the junction temperature as computed using (11.1) is less than the maximum junction temperature T_J,MAX as specified by the manufacturer, then the device is expected to perform safely as approved by its manufacturer.

The manufacturer also specifies the maximum power a device can dissipate at room temperature (usually 25 C). The power rating of the device remains at its maximum as long as the operating temperature is lower than or equal to 25 C. As the ambient temperature increases, the power rating of the device decreases.

Let us suppose that a transistor is rated at 5 W at a room temperature of 25 C, its junction-to-air thermal resistance is q_JA C/W, and its maximum junction temperature is 200 C. This simply means that the transistor can safely dissipate 5 W when the ambient temperature is less than or equal to 25 C. In addition, when it is dissipating power its junction temperature should be less than or at the most equal to 200 C for safe operation. As the transistor dissipates power, it junction temperature rises in accordance with (11.1).

For example, when the room temperature is 25 C, the junction temperature becomes 60 C when it dissipates 1 W. The junction temperature rises to 95 C as it dissipates 2 W. In other words, the junction temperature rises 35 C above the ambient temperature for each watt of power dissipated by the transistor. Finally, the junction temperature reaches 200 C as the transistor dissipates 5 W at a room temperature of 25 C.

What we have just stated can also be stated in the following way. If the ambient temperature is already at 60 C, the transistor can only dissipate 4 W of power. Likewise, if the ambient temperature is already at 95 C, the transistor can only dissipate 3 W of power. In the end when the ambient temperature reaches 200 C, the transistor cannot safely dissipate any power at all. Simply put, as the ambient temperature rises, the power dissipation capability of the transistor decreases. This decrease in power rating is sketched in Figure 11.1. The curve is usually called the derating curve of the device (transistor in our example).

When the manufacturer of the device does not provide any information on its thermal resistance, the manufacturer then supplies the necessary derating curve of the transistor.

Ambient temperature

Figure 11.1: Power dissipation as a function of ambient temperature

As you can see, the transistor has a maximum power rating of 5 W up to an ambient temperature of 25 C. Thereafter, the power rating drops as the temperature rises. Once the junction temperature reaches 200 C (an increase of 175 C from the ambient), the power rating drops to zero.

Example 1: Junction Temperature Calculations _____ _______ ______ _________

The maximum power rating of a transistor at 25 C is 5 W. Its junction-to-air thermal resistance is 35 C/W and its maximum junction temperature is 200 C. The transistor is used in a design where it has to dissipate 2 W when the ambient temperature is 75 C. Is it safe to use this transistor?

Solution:

For our application, the ambient temperature is given as 75 C and the transistor has to dissipate 2 W, its junction temperature, from (11.1), should be

T_J = 75 + 2 C

The junction temperature is considerably lower than the maximum junction temperature of 200 C. The transistor will be able to maintain its cool (couldnt resist to say so) all by itself.

GENERAL CONSIDERATIONS

For designs using silicon active devices such as transistors and diodes, the maximum junction temperature must not exceed 110 C for ground and airborne applications. If the maximum rated junction temperature of the device by its manufacturer is £ C, the maximum junction temperature for missile-flight applications must not exceed 110 C. If the maximum rated temperature of the device is ³ C, the maximum junction temperature for missile-flight applications must not exceed 140 C.

The transistor in Example-1 does not meet the above guidelines because its junction temperature is 145 C. We should develop methods to cool it down.

THERMAL MODEL

Equation (11.1) can also be written as

T_J - T_A = P_D q_JA (11.2)

where T_J - T_A is the rise in the temperature of the junction with respect to the ambient temperature (air). If we treat the rise in temperature as the voltage, the power dissipated by the transistor as the current, and its thermal resistance as the resistance, then the above equation is simply a statement of Ohms law. We may now represent this equation by an equivalent circuit as given in Figure 11.2. We will have more to say about this thermal model (equivalent circuit) later.

Figure 11.2: Thermal model of a transistor

COOLING METHODS

The simplest cooling method is a heat sink. A heat sink is made of a good thermally conducting material and has a large surface area. The aim is to mount the power transistor on the heat sink. Since the case is the collector terminal of a power transistor, a thin insulator (insulating washer) is used to separate the case from the sink. The thermal resistance of an insulator depends upon the material used for the heat sink and its size. When the heat sink is electrically isolated from the rest of the circuit, then the insulator can be dispensed with. Thermal resistances q_JS, C/W) of some of the commonly used insulators are given in Table-1.

Insulator Thickness, in q_JS, C/W

No insulation ----- ----- -------- 0.4

Anodized aluminum 0.016 0.4

0.125 0.5

Mica 0.002 0.5

0.004 0.65

Mylar 0.003 1.0

Glass cloth (Teflon coated) 0.003 1.25

Heat sinks also come in various sizes and shapes. The thermal resistance (q_SA C/W) of a heat sink varies roughly between 1 C/W to 10 C/W depending upon its size, shape, material, surface finish, and orientation to the air flow. The smaller the rating number, the better the heat sinking process. The thermal resistances and other pertinent information on various types of heat sinks are given in Table 2. All dimensions are in inches, surface area (S) is in in², and displacement volume (V) is in in³. In the table below, L, W, and H are the length, width, and height, respectively. In addition, Wt is the weight of the heat sink in grams.

Volume displacement

S L W H V Wt Finish q_SA C/W

Flat-finned Extrusion

1 65 3.0 3.6 1.0 10.8 114 Anodized black 2.4

2 Bright Aluminum 3.0

3 Gray Aluminum 2.8

4 60 3.0 4.0 0.69 8.3 123 Anodized black 2.8

5 95 3.0 4.0 1.28 15.3 189 Anodized black 2.1

6 64 3.0 3.8 1.3 15.0 155 Black paint 2.2

7 83 3.0 4.0 1.25 15.0 140 Anodized black 2.2

8 44 1.5 4.0 1.25 7.5 75 Anodized black 3.0

9 137 3.0 4.0 2.63 31.5 253 Anodized black 1.45

10 250 5.5 4.0 2.63 58.0 461 Anodized black 1.10

11 130 6 3.6 1.0 21.5 253 Anodized black 1.75

12 78 3.0 3.8 1.1 12.5 190 Anodized gray 2.9

13 62 3.0 3.8 1.3 15.0 170 Anodized gray 2.2

14 78 3.0 4.5 1.0 13.5 146 Gold Alodine 3.0

Cylindrical-fins, Horizontal Machined Casting

15 30 1.75 * 0.84 2.0 40 Anodized black 8.5

16 50 1.75 * 1.5 3.6 67 Anodized black 7.1

17 37 1.75 * 1.5 3.6 48 Anodized black 6.65

Cylindrical-fins, Vertical Casting

18 7.5 1.5 * 0.9 4.4 33 Anodized black 8.1

19 12 1.5 * 1.4 6.9 51 Anodized black 7.0

20 25 1.5 * 2.9 14.2 112 Anodized black 5.6

21 35 1.5 * 3.4 16.7 132 Anodized black 5.1

22 32 2.5 * 1.5 7.4 94 Anodized black 4.5

23 20 2.5 * 0.5 2.45 48 Anodized black 6.6

Flat-fins, Casting

24 23 1.86 1.86 1.2 4.15 87 Anodized black 5.06

Vertical fins, Square Sheet Metal

25 12 1.7 1.7 1.0 2.9 19 Anodized black 7.4

Cylindrical Sheet metal

26 15 2.3 * 0.81 3.35 18 Black paint 7.1

Horizontal fins, cylindrical Sheet Metal

27 6 1.81 * 0.56 1.44 20 Anodized black 9.15

* Diameter

Example 2: Low Power Transistor __________ ______ ____ _____________

A low-power germanium transistor has a thermal (junction-to-air) resistance of 0.5 C/mW and its maximum allowable temperature is 85 C. Determine the amount of power it can safely dissipate when the room temperature is (a) 25 C, and (b) 60 C.

Solution:

(a) From (11.2), the permissible power dissipation by the transistor at an ambient temperature of 25 C is

(b) When the ambient temperature is 60 C, the maximum power dissipation capability of the transistor is

Once again, this example shows that the increase in the ambient temperature limits the amount of power that a transistor can safely dissipate.

DERATE FACTOR

It is also common to express the power dissipation capability of a device (especially for a low power device) in terms of the derate factor. The derate factor is simply the inverse of the thermal resistance. For low power devices, it is usually given in terms of mW/ C. It stresses the fact that as the temperature increases beyond the specified ambient temperature of the device, its maximum power rating must be reduced in accordance with its derate factor. For the transistor data given in Example-2, the derate factor is 2 mW/ C (1 q_JA). It simply means that for every one-degree increase in the ambient temperature of the transistor, its power rating goes down by 2 mW. Thus, when the ambient temperature reaches 60 C, the maximum power rating of the transistor would be

= 120 (2)(60 - 25) = 50 mW

Although the transistor is rated at 120 mW at 25 C, it must be derated to 50 mW at 60 C. The maximum power it can safely dissipate at the ambient temperature of 60 C is 50 mW.

MODIFIED THERMAL MODEL

When the device (such as a transistor) is mounted on the heat sink, the heat flows from the junction of the device to its case, then from the case to the heat sink through the insulator, and finally from the heat sink to the surrounding air. Base upon this understanding, we can develop an equivalent thermal model of the device as shown in Figure 11.3.

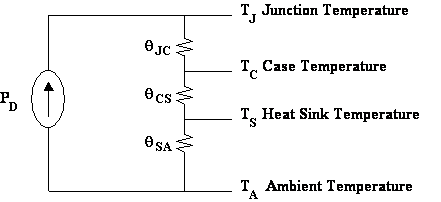
Figure 11.3: Thermal Model of a device including insulator and heat sink

In the thermal model of Figure 11.3 P_D is the power being dissipated by the device, T_J is the junction temperature, T_C is the case temperature, T_S is the heat sink temperature, and T_A is the ambient temperature. In addition, q_JC is the junction-to-case thermal resistance of the device, q_CS is the case-to-sink thermal resistance of the insulator, and q_SA is the thermal resistance from sink-to-air of the heat sink. From the thermal model of Figure 11.3, it is clear that the temperature of the junction with respect to the case is

(11.3)

Likewise, the temperature of the case with respect to the ambient is

(11.4)

Finally, we can express the junction temperature in terms of the ambient temperature as

(11.5)

Equation (11.4) is useful when the manufacturer of the device specifies the maximum allowable case temperature. This is done with an understanding that when the case temperature is below the maximum specified limit, the junction temperature would automatically be below its maximum limit. In this case, we dont have to compute the junction temperature. The device will operate safely as long as the case temperature is maintained below its maximum specified value.

Example 3: Power Diode __________ ______ ____ _____ _______ ______ ________

The maximum case temperature of a 10-W power diode is specified as 110 C. Its junction-to-case thermal resistance is 3 C/W. It is mounted on a heat sink with a thermal resistance of 8.5 C/W. The insulator has a thermal resistance of 0.5 C/W. The forward voltage drop across the diode is 0.8 V. Determine the maximum current the diode can safely carry when the ambient temperature is 45 C. Also compute its junction temperature.

Solution:

Since we have to abide by the temperature limit on the case of the diode, we use (11.4) for our calculation. Although the diode is rated at 10-W, it may not be able to dissipate 10-W of power for the given heat sink and the insulator. We can determine the maximum power that the diode can dissipate using (11.4). If the maximum power as computed from (11.4) is higher than 10-W, the current calculations can then be based upon its power dissipation capability of 10 W. If the maximum power as computed from (11.4) is less than 10 W, then we should use the computed power to determine the maximum current carrying capability of the diode.

The safe limit on the power based on (11.4) is

Since P_D is less than 10 W, the maximum limit on the power dissipation by the diode is 7.22 W. Therefore, the maximum current carrying capability of the diode is

The diodes operation is safe as long as the ambient temperature is less than or equal to 45 C and its current is less than or equal to about 9 A.

When the case is at its maximum temperature of 110 C, we can compute the junction temperature using (11.3). That is

Example 4: Selection of a Heat Sink for a Power Diode _____ _______ ______ ______________

Select another heat sink that would enable the diode in Example-3 to dissipate its rated power of 10 W.

Solution: From (11.4), we obtain

When we use the same insulator, the maximum thermal resistance of the heat sink should be

We can select a heat sink that is compatible with the diode from Table-2. The thermal resistance of the heat sink must be less than or equal to 6 C/W. The #20 heat sink appears to satisfy our requirement. We can use it as long as the diode can be easily mounted on it.

Example 5: Heat Sink Selection for a Power Transistor _____ _______ ______ ____________

Typical data on an RCA-40322 power transistor is given in Table-11.3. The transistor is used as a power amplifier for class-B configuration. The transistor has to dissipate 10 W of power. (a) Select a heat sink based upon its maximum junction temperature. (b) Select the heat sink if the amplifier is a part of missile-flight system. Assume that the ambient temperature is 50 C.

Solution:

As given in Table-3, the transistor can dissipate 35 W as long as its case temperature is 25 C. The maximum junction temperature is also specified as 200 C. Thus, the thermal resistance of the device is q_JC C/W. The derate factor is 0.2 W/ C. The maximum power rating of the transistor at 50 C is

First of all, the transistor has to be derated from its maximum power dissipation capability of 35 W at 25 C to its new maximum power dissipation capability of 30 W at a case temperature of 50 C. As the case temperature rises, the maximum power dissipation capability of the transistor decreases at the rate of 0.2 W/ C.

(a) Let q_T be the total thermal resistance such that

Let us also select an anodized aluminum washer with q_CS C/W.

Table-3: Data on RCA-40322 Power Transistor

For a maximum junction temperature of 200 C and required power dissipation of 10 W, we obtain the total thermal resistance as

Thus, the maximum thermal resistance of the heat sink is

From Table-2, we can either select #27 or #15. Selection of #15 gives us a higher safety factor than that of #27. Let us select #27, cylindrical horizontal fins, sheet metal with anodized black finish. It has a thermal resistance of 9.15 C/W.

With this heat sink, the expected temperature of the case is

T_C C

At this temperature, the maximum power dissipation capability of the transistor is

As you may have suspected, there is no room for error in this case.

(b) When the junction temperature is limited to 140 C, then the total thermal resistance is

Thus, the maximum thermal resistance of the heat sink is

From Table-2, we can either select #2, #8, or #14. Each selection has a thermal resistance of 3 C/W. With this heat sink, the expected temperature of the case is

T_C C

At this temperature, the maximum power dissipation capability of the transistor is

A direct comparison reveals that the heat sink selected in part (b) weighs more and has larger dimensions than that in part (a). However, it provides a safety factor of 2.3. This is the kind of tug of war a designer faces at all times. Cost on one side and safety requirements on the other. Which one wins, only the designer knows!

(END OF DISCUSSION)